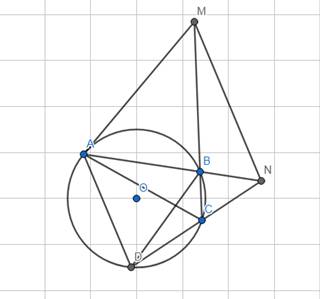
Cho tứ giác \(ABCD\)nội tiếp đường tròn\(\left(O\right)\)
A) Chứng minh : \(\widehat{BAC}=\widehat{DBC}+\widehat{BDC}\)
B) Gỉa sử hai cạnh AB và CD bằng nhau. Tứ giác\(ABCD\)là hình gì ? Chứng minh.
C) Gỉa sử hai đường chéo AC và BD vuông góc với nhau tại \(I\). Gọi M là trung điểm của BC, N là trung điểm của AD. Chứng minh OM=IN
( GIÚP MÌNH VỚI Ạ )