Cho điểm A là một điểm nằm bên ngoài đường tròn (O), gọi AB và AC lần lượt là hai tiếp tuyến tại B và C của đường tròn (O), vẽ cát tuyến ADE của đường tròn (O) ( Biết điểm D nằm giữa hai điểm A và E, đường thẳng AE không đi qua điểm O).1) Chứng minh tứ giác ABOC là tứ giác nội tiếp đường tròn. Xác định tâm của đường tròn ngoại tiếp tứ giác ABOC.2) Chứng minh : AB2=AD.AE3) ...
Đọc tiếp
Cho điểm A là một điểm nằm bên ngoài đường tròn (O), gọi AB và AC lần lượt là hai tiếp tuyến tại B và C của đường tròn (O), vẽ cát tuyến ADE của đường tròn (O) ( Biết điểm D nằm giữa hai điểm A và E, đường thẳng AE không đi qua điểm O).
1) Chứng minh tứ giác ABOC là tứ giác nội tiếp đường tròn. Xác định tâm của đường tròn ngoại tiếp tứ giác ABOC.
2) Chứng minh : AB2=AD.AE
3) Đường thẳng đi qua điểm C song song với đường thẳng AE cắt đường tròn (O) tại điểm M, với M khác C. Gọi H là giao điểm của hai đường thẳng BM và AE. Chứng minh HD = HE
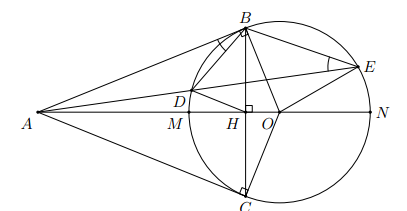hình
1) Ta có \(\widehat{ABO}=\widehat{ACO}=90độ\left(gt\right)\)
Do đó\(\widehat{ABO}+\widehat{ACO}=180độ\)
Nên tứ giác ABOC nội tiếp đường tròn đường kính AO
Tâm đường tròn ngoại tiếp tứ giác ABOC là trung điểm AO.
2) Xét ΔABD và ΔAEB có
\(\widehat{BAE}\)chung
\(\widehat{ABD}=\widehat{AEB}\)(góc tạo bởi tia tiếp tuyến và dây và góc nội tiếp cùng chắn \(\widebat{BD}\))
Nên ΔABD
ΔAEB
Do đó \(\frac{AB}{AE}\)=\(\frac{AD}{AB}\)
Hay AB2= AE.AD