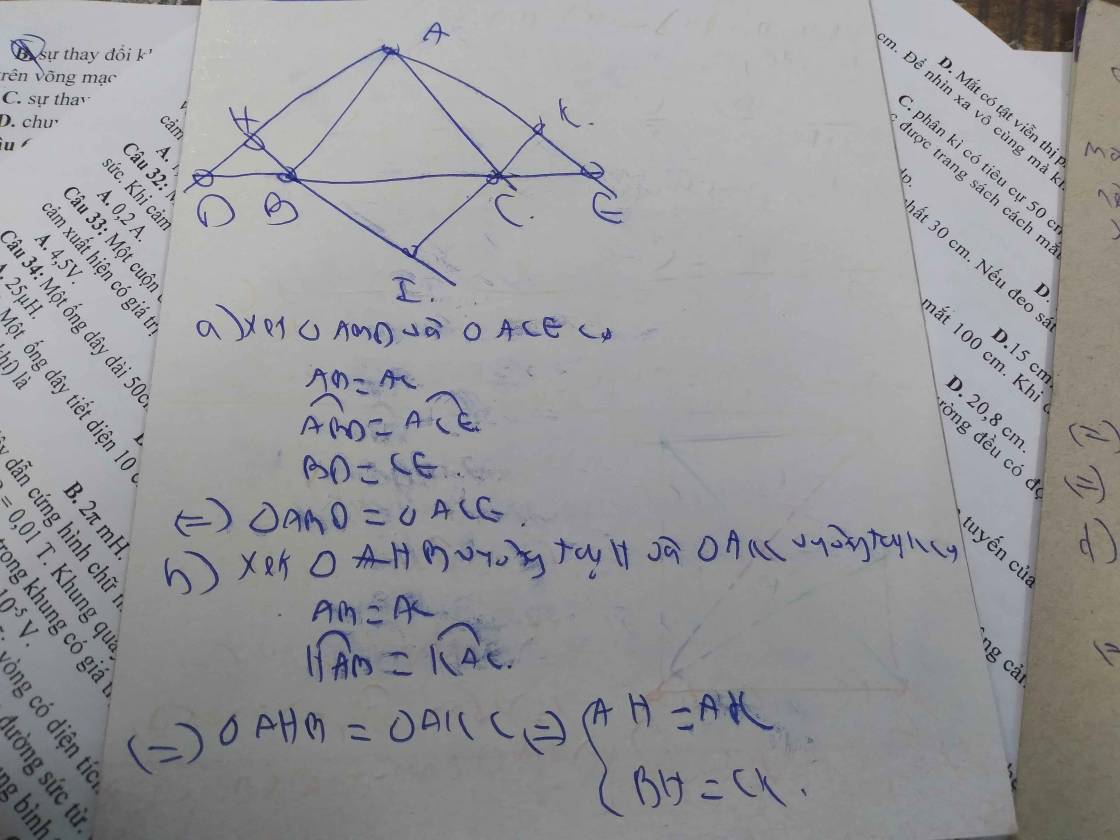
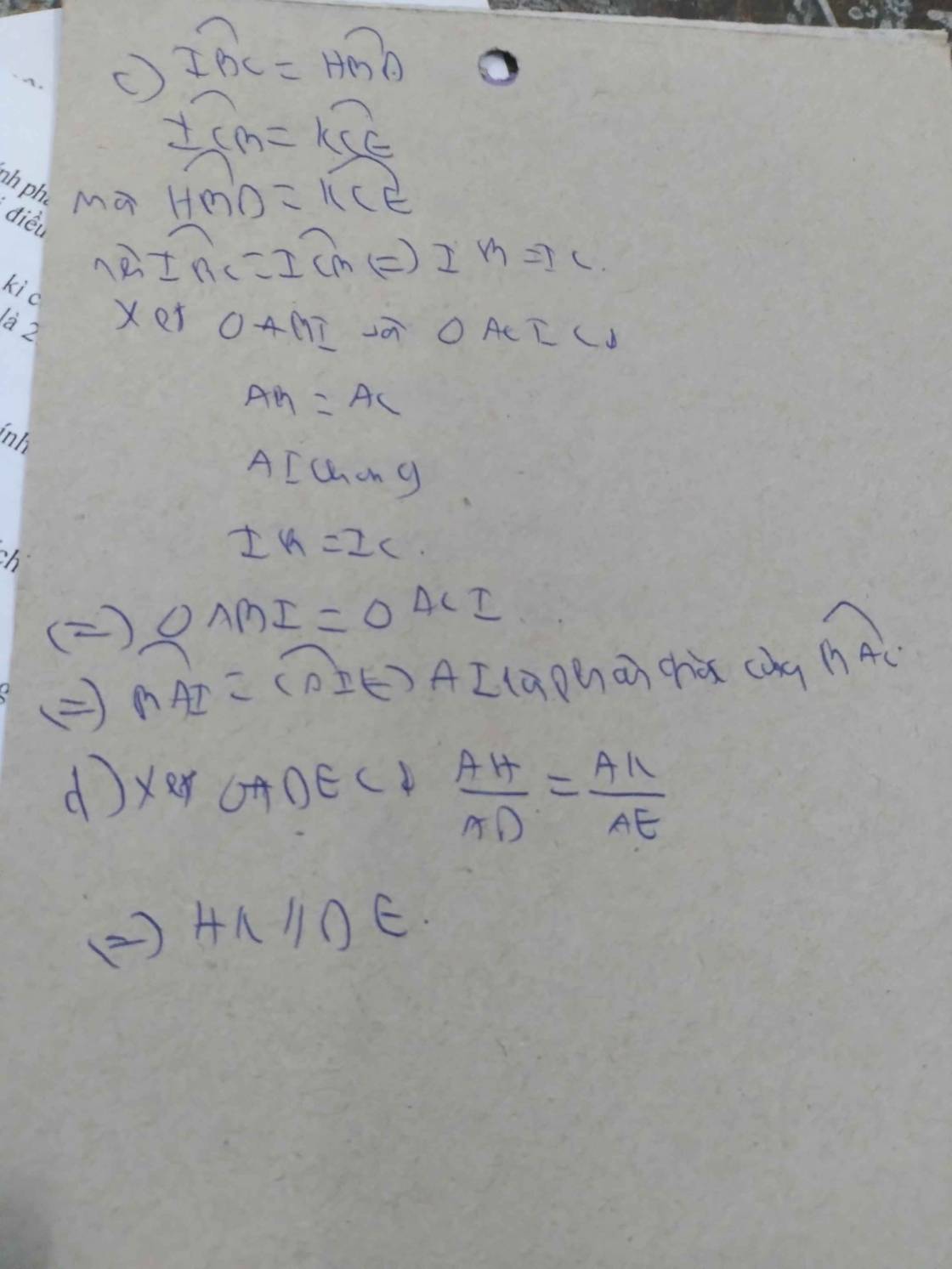Cho tam giác ABC cân. Trên tia đối BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE
a) Góc ABD = góc ACE
b) Góc DAB = góc CAE
c) Vẽ BH vuông góc với AD ( H thuộc AD ), vẽ CK vuông góc với AE ( K thuộc AE ). Chứng minh BH = CK; góc HBD = góc kcs
d) Tia HB cắt KC tại I. Chứng minh AI là phân giác của góc BAC