ông sáu guu 1 số tiền vào ngân hàng theo mức lãi suất tiết kiệm với kì hạn 1 năm là 6%. tuy nhiên sau thời hạn 1 năm ông sau ko đến nhận tiền lại mà để thêm 1 năm nữa mới lanh . khi đó số tiền lại có...

JB

Jenny Brown

18 tháng 4 2018 - olm

ông sáu guu 1 số tiền vào ngân hàng theo mức lãi suất tiết kiệm với kì hạn 1 năm là 6%. tuy nhiên sau thời hạn 1 năm ông sau ko đến nhận tiền lại mà để thêm 1 năm nữa mới lanh . khi đó số tiền lại có được sau năm đầu tiên sẽ được ngân hàng cộng dồn vào số tiền gửi ban đầu để thành số tiền gửi cho năm kế tiếp với mức lãi suất cũ . sau 2 năm ông sáu nhận được số tiền là...

Đọc tiếp

#Toán lớp 8

0

TT

Tam Tứ Tình

26 tháng 7 2016

Ông Sáu gửi một số tiền vào ngân hàng theo mức lãi suất tiết kiệm với kỳ hạn 1 năm là 6%. Tuy nhiên sau thời hạn một năm ông Sáu không đến nhận tiền lãi mà để thêm một năm nữa mới lãnh. Khi đó số tiền lại có được sau năm đầu tiên sẽ được ngân hàng cộng dồn vào số tiền gửi ban đầu để thành số tiền gửi cho năm kế tiếp với mức lãi suất cũ. Sau 2 năm ông Sáu nhận...

Đọc tiếp

#Toán lớp 10

2

NN

Nguyễn Ngọc Như Quỳnh

26 tháng 7 2016

Giải:

Gọi số tiền ông Sáu gửi ban đầu là x.

Theo đề bài ta có:

Số tiền lãi sau 1 năm ông Sáu nhận được là : 0,06x (đồng)

Số tiền lãi có được 1 năm của ông Sáu là : x + 0,06x = 1,06x (đồng)

Số tiền lãi năm thứ 2 ông Sáu nhận được là : 1,06x. 0,06 = 0,0636x (đồng)

Do vậy, số tiền tổng cộng sau 2 năm ông Sáu nhận được là : 1,06x + 0,0636x = 1,1236x (đồng)

Mặt khác: 1,1236x = 112360000 nên x = 100000000(đồng) hay 100 triệu đồng

Vậy ban đầu ông Sáu đã gửi 100 triệu đồng.

Đúng(0)

LN

Lê Nguyên Hạo

26 tháng 7 2016

Tổng % lãi suất trong 2 năm là :

6% . 2 = 12%

Số tiền lãi trong 2 năm là :

112360000 . 12% = 13483200

=> Tiền ông Sáu gửi là :

112360000 - 13483200 = 98876800

Đúng(0)

TT

Tam Tứ Tình

25 tháng 7 2016

a) Thu gọn biểu thức sau: A = \(\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\)b) Ông Sáu gửi một số tiền vào ngân hàng theo mức lãi xuất tiết kiệm với kỳ hạn 1 năm là 6%. Tuy nhiên sau thời hạn một năm ông Sáu không đến nhận tiền lãi mà để thêm 1 năm nữa mới lãnh. Khi đó số tiền lãi có được sau năm đầu tiên sẽ được ngân hàng cộng dồn vào số tiền gửi ban...

Đọc tiếp

#Toán lớp 10

2

TV

Trần Việt Linh

25 tháng 7 2016

a) \(A=\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}+\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\)

\(=\frac{2-\sqrt{3}}{1+\sqrt{\left(\sqrt{3}+1\right)^2}}+\frac{2+\sqrt{3}}{1-\sqrt{\left(\sqrt{3}-1\right)^2}}\)

\(=\frac{2-\sqrt{3}}{1+\sqrt{3}+1}+\frac{2+\sqrt{3}}{1-\sqrt{3}+1}\)

\(=\frac{2-\sqrt{3}}{2+\sqrt{3}}+\frac{2+\sqrt{3}}{2-\sqrt{3}}\)

\(=\frac{\left(2-\sqrt{3}\right)\left(2-\sqrt{3}\right)+\left(2+\sqrt{3}\right)\left(2+\sqrt{3}\right)}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)

\(=\frac{4-4\sqrt{3}+3+4+4\sqrt{3}+3}{4-3}\)

\(=14\)

Đúng(0)

NN

Nguyễn Ngọc Như Quỳnh

25 tháng 7 2016

a) A = \(\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{3+2\sqrt{3.1+1}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{3-2\sqrt{3.1+1}}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{\left(\sqrt{3+1}\right)^2}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{\left(\sqrt{3-1}\right)^2}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{3+1}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{3+1}}\) = \(\frac{2-\sqrt{3}}{2+\sqrt{3}}\) + \(\frac{2+\sqrt{3}}{2-\sqrt{3}}\) = \(\frac{\left(4-4\sqrt{3+3}\right)+\left(4+4\sqrt{3+3}\right)}{4-3}\) = \(\frac{14}{1}\) = 1

Đúng(0)

TD

tran duy anh

7 tháng 8 2018 - olm

Bà Dung gửi một số tiền vào ngân hàng theo mức lãi suất tiết kiệm với kỳ hạn 1 năm 6%. Tuy nhiên sau thời hạn 1 năm, bà Dung không đến nhận tiền lãi mà phải thêm 1 năm nữa mới lãnh. Khi đó số tiền lãi có được sau năm đầu tiên sẽ được ngân hàng cộng dồn vào số tiền ban đầu thành số tiền gửi cho năm kế tiếp với mức lãi suất cũ. Sau 2 năm bà Dung nhận được số tiền là 56180000...

Đọc tiếp

#Toán lớp 8

3

NT

Nguyễn Tũn

7 tháng 8 2018

Hãy tích cho tui đi

vì câu này dễ mặc dù tui ko biết làm

Yên tâm khi bạn tích cho tui

Tui sẽ ko tích lại bạn đâu

THANKS

Đúng(0)

TD

tran duy anh

7 tháng 8 2018

Dễ rồi thì phải nghĩ ra cách gì để giải chứ

Đúng(0)

PD

Pain do

14 tháng 3 2022

Ông Hải sau khi tiết kiệm được một số tiền đã mang đến một ngân hàng để gửi tiết kiệm theo kì hạn 6 tháng với lãi suất 6%/năm. Sau một năm, ông nhận lại được số tiền là 5 304 500 đồng. Hỏi lúc đầu ông Hải đem gửi ngân hàng bao nhiêu tiền, biết rằng ông Hải không rút tiền lãi và tiền lãi được cộng vào tiền gốc để tính lãi cho kì hạn tiếp...

Đọc tiếp

#Toán lớp 8

0

PT

Pham Trong Bach

19 tháng 3 2018

Ông An có 200 triệu đồng gửi tiết kiệm tại ngân hàng với kì hạn 1 tháng so với lãi suất 0,6%/ 1 tháng được trả vào cuối kì. Sau mỗi kì hạn ông đến tất toán cả gốc lẫn lãi, rút ra 4 triệu đồng để tiêu dùng, số tiền còn lại ông gửi vào ngân hàng theo phương thức trên (phương thức giao dịch và lãi suất không thay đổi trong suốt quá trình gửi). Sau đúng 1 năm (đúng 12 kì hạn) kể từ...

Đọc tiếp

#Mẫu giáo

2

CM

Cao Minh Tâm

19 tháng 3 2018

Sau tháng thứ nhất, số tiền còn lại là

Sau tháng thứ hai số tiền còn lại là

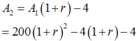
Sau 12 tháng số tiền còn lại là

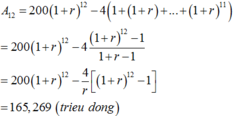
Chọn D.

Đúng(0)

NT

Nguyễn Thị Hà Chi

4 tháng 1

Sau tháng thứ nhất, số tiền còn lại là

Sau tháng thứ hai số tiền còn lại là

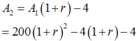
Sau 12 tháng số tiền còn lại là

Đúng(0)

TN

thanh nguyên Lê nguyễn

30 tháng 4 2023

Bài 3 Ông Sáu gửi 500 triệu đồng vào ngân hàng A với kì hạn 1 năm .Biết lãi suất gửi kì hạn một năm của ngân hàng A là 5%a) Hỏi sau một năm ông Sáu nhận được số tiền lãi là bao nhiêu?b) Em hãy tính tỉ số phần trăm giữa tiền gửi ban đầu và số tiền nhận được (cả vốn lẫn lãi) sau một năm của ông...

Đọc tiếp

#Toán lớp 6

1

NA

Nguyễn An Ninh

VIP

30 tháng 4 2023

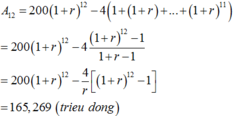
a) Số tiền lãi mà ông Sáu nhận được sau 1 năm là:

= 500 triệu x 0.05 x 1 = 25 triệu đồng

b) Tỉ số phần trăm giữa tiền gửi ban đầu và số tiền nhận được (cả vốn lẫn lãi) sau 1 năm của ông Sáu là:

\(\dfrac{103}{250}\)

Tổng số tiền ông Sáu nhận được sau 1 năm là:

525 triệu / 500 triệu x 100% = 105%

Vậy tỉ số phần trăm giữa tiền gửi ban đầu và số tiền nhận được (cả vốn lẫn lãi) sau 1 năm của ông Sáu là 105%.

Đúng(2)

MT

Minh thư Trần

7 tháng 11 2023

Bài 5. Ông Phú gửi tiết kiệm 100 triệu đồng tại một ngân hàng với kì hạn một năm, lãi suất 5% một năm. Hết thời hạn một năm, tiền lãi gộp vào số tiền gửi ban đầu và lại gửi theo thể thức cũ. Cứ như thế sau ba năm thì số tiền cả gốc lẫn lãi là bao nhiêu?SOS mn...

Đọc tiếp

#Toán lớp 7

2

CH

Cee Hee

7 tháng 11 2023

Số tiền cả gốc lẫn lãi sau 1 năm là:

\(100000000\cdot\left(1+5\%\right)=105000000\left(đ\right)\)

Số tiền cả gốc lẫn lãi sau 2 năm tiếp là:

\(105000000\cdot\left(1+5\%\right)=110250000\left(đ\right)\)

Số tiền cả gốc lẫn lãi sau 3 năm tiếp là:

\(110250000\cdot\left(1+5\%\right)=115762500\left(đ\right)\)

Vậy: Cứ như thế sau ba năm thì số tiền cả gốc lẫn lãi là \(115762500\) đồng

(\(100\%=\dfrac{100}{100}=1\)).

Đúng(3)

MT

Minh thư Trần

7 tháng 11 2023

Cảm ơn ạ

Đúng(0)

PT

Pham Trong Bach

15 tháng 8 2018

Ông An gửi 100 triệu đồng vào ngân hàng với hình thức lãi kép, kỳ hạn 1 năm với lãi suất 8%/năm. Sau 5 năm ông rút toàn bộ tiền và dùng một nửa để sửa nhà, số tiền còn lại ông tiếp tục gửi vào ngân hàng với kỳ hạn và lãi suất như lần trước. Số tiền lãi mà ông An nhận được sau 10 năm gửi gần nhất với giá trị nào sau đây? A. 34,480 triệu. B. 81,413 triệu. C. 107,946 triệu. D. 46,933...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

15 tháng 8 2018

Đáp án A

Phương pháp:

Công thức lãi kép, không kỳ hạn: An = M(1 + r%)n

Với:

An là số tiền nhận được sau tháng thứ n,

M là số tiền gửi ban đầu,

n là thời gian gửi tiền (tháng),

r là lãi suất định kì (%)

Cách giải:

Số tiền ông An rút lần 1 là: 100.(1 + 8%)5 = 146,9328077 (triệu đồng)

Số tiền ông An gửi lần 2 là: 146.9328077 : 2 = 73,46640384 (triệu đồng)

Số tiền ông An rút lần 2 (gửi 5 năm tiếp theo) là:

73,46640384.(1 + 8%)5 = 107,9462499 (triệu đồng)

Số tiền lãi là: 107,9462499 - 73,4660384 = 34,47984602 ≈ 34,480 (triệu đồng).

Đúng(0)

PT

Pham Trong Bach

27 tháng 11 2019

Ông An gửi tiết kiệm 50 triệu đồng vào ngân hàng với kỳ hạn 3 tháng, lãi suất 8,4% một năm theo hình thức lãi kép. Ông gửi được đúng 3 kỳ hạn thì ngân hàng thay đổi lãi suất, ông gửi tiếp 12 tháng nữa với kỳ hạn như cũ và lãi suất trong thời gian này là 12% một năm thì ông rút tiền về. Số tiền ông An nhận được cả gốc lẫn lãi tính từ lúc gửi tiền ban đầu là: (làm tròn đến...

Đọc tiếp

#Mẫu giáo

2

CM

Cao Minh Tâm

27 tháng 11 2019

Đáp án D

Số tiền mà ông An nhận được là

T = 50.10 6 . 1 + 8 , 4 4 % 3 . 1 + 12 4 % 4 ≈ 59.895.767 đ ồ n g .

Đúng(0)

NT

Nguyễn Thị Hà Chi

4 tháng 1

Đáp án D

Số tiền mà ông An nhận được là

T = 50.10 6 . 1 + 8 , 4 4 % 3 . 1 + 12 4 % 4 ≈ 59.895.767 đồng .

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP