Cho tam giác DEF có: \(12\widehat{D}=10\widehat{E}=15\widehat{F}\)
a, So sánh các cạnh của tam giác DEF
b, Phân giác của góc E cắt DF tại M. So sánh DM và FM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 6 2022
a: Đặt \(\widehat{D}=a;\widehat{E}=b;\widehat{F}=c\)
Theo đề, ta có: 12a=10b=15c
=>a/5=b/6=c/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{6}=\dfrac{c}{4}=\dfrac{a+b+c}{5+6+4}=\dfrac{180}{15}=12\)
Do đó:a=60; b=72; c=48
Xét ΔDEF có \(\widehat{F}< \widehat{D}< \widehat{E}\)
nên DE<FE<FD
b: Xét ΔDEF có EM là phân giác
nên DM/DE=MF/EF
mà DE<EF
nên DM<MF
TP
28 tháng 8 2017
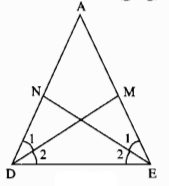
Tam giác ADE có: \(\widehat{\text{D}}=\widehat{E}\)(gt)
\(\widehat{\text{D1}}=\widehat{D2}=\dfrac{1}{2}\widehat{D}\)(Vì DM là tia phân giác)
\(\widehat{\text{E1}}=\widehat{E2}=\dfrac{1}{2}\widehat{E}\)(Vì EN là tia phân giác)
Suy ra:\(\widehat{\text{D1}}=\widehat{D2}=\)\(\widehat{\text{E1}}=\widehat{E2}\)
Xét ∆DNE = ∆EMD, ta có:
\(\widehat{NDE}\widehat{=MED}\)((gt)
DE cạnh chung
\(\widehat{\text{D1}}=\widehat{E2}=\)(chứng minh trên)
Suy ra: ∆DNE = ∆EMD (g.c.g)
Vậy DE = EM (2 cạnh tương ứng).
DT
10 tháng 5 2022
a) Có DE < DF( 5cm < 12cm)
->góc F< góc E
b) áp dụng đl pytago:
EF^2=DE^2+DF^2=5^2+12^2=169
= > EF=13 (cm)
tam giác DEF có DM là trung tuyến(M là trung điểm của EF) ứng với cạnh huyền
=> DM=EM=MF=EF/2=13/2=6,5cm
17 tháng 9 2023
a)
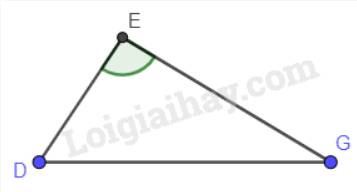
Trong tam giác DEG có góc E là góc tù (góc > 90°). Mà DG là cạnh đối diện với góc E nên DG là cạnh lớn nhất trong tam giác.
Vậy DE < DG.
b)
Tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Mà tổng ba góc trong một tam giác bằng 180°. Vậy \(\widehat P = 180^\circ - 56^\circ - 65^\circ = 59^\circ \).
Ta thấy: \(\widehat M < \widehat P < \widehat N\). Hay cạnh nhỏ nhất của tam giác MNP là NP (đối diện với góc M), cạnh lớn nhất của tam giác MNP là MP (đối diện với góc N).
a/ Ta có \(12\widehat{D}=15\widehat{F}\)
=> \(4\widehat{D}=5\widehat{F}\)
=> \(\widehat{D}=\frac{5}{4}\widehat{F}\)
=> \(\widehat{D}>\widehat{F}\)(1)
và \(10\widehat{E}=15\widehat{F}\)
=> \(2\widehat{E}=3\widehat{F}\)
=> \(\widehat{E}=\frac{3}{2}\widehat{F}\)
=> \(\widehat{E}>\widehat{F}\)(2)
Từ (1) và (2) => \(\widehat{D}>\widehat{E}>\widehat{F}\)
=> EF > DF > DE (quan hệ giữa góc và cạnh đối diện trong tam giác)