Không liên quan lắm nhưng mọi người cho mình hỏi làm thế nào để tham gia cuộc thi "Cuộc thi Toán Tiếng Anh VEMC mùa 4 (by Cuộc thi Trí tuệ VICE)" với ạ, mình tìm mãi mà không thấy nút để ấn thâm gia ở đâu ấy...Cảm ơn mọi người nhiềuu^^
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
6 tháng 5 2021
Ngoài ra chúng mình cũng cần tìm thêm nhà tài trợ phụ ngoài nhà tài trợ chính là hoc24.vn ^^ Ai có thể giới thiệu cho chúng mình nhỉ?
MN
6 tháng 5 2021
đề xuất với ad cho tổ chức cuộc thi thiết kế như cuộc thi thiết kế logo nhé =)))
24 tháng 6 2021
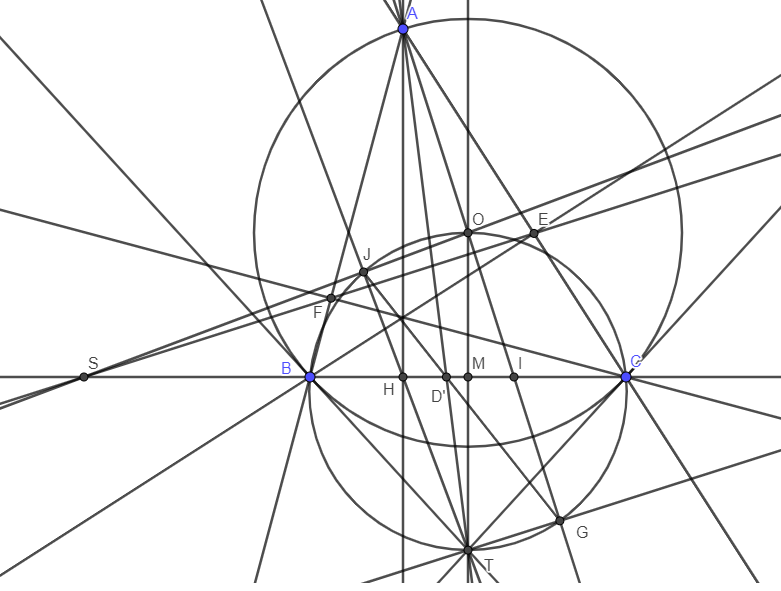
a) Theo phương tích ta có HB . HC = HJ . HT. (1)
Mặt khác do (BCHS) = -1 nên theo hệ thức Maclaurin ta có HB . HC = HM . HS. (2)
Từ (1), (2) suy ra HM . HS = HJ . HT, do đó tứ giác SJMT nội tiếp.
b) Theo hệ thức lượng ta có \(MO.MT=MB^2\).
Mặt khác theo hệ thức Newton, ta có \(MB^2=MH.MS\).
Do đó \(MO.MT=MH.MS\Rightarrow\dfrac{MO}{MS}=\dfrac{MH}{MT}\Rightarrow\Delta MOS\sim\Delta MHT\left(c.g.c\right)\).
Từ đó \(\widehat{MSO}=\widehat{MTH}\Rightarrow SO\perp TH\).
Lại có tứ giác SJMT nội tiếp nên \(\widehat{SJH}=90^o\). Suy ra S, J, O thẳng hàng.
JG cắt BC tại D'. AO cắt BC tại I.
Ta có \(\dfrac{D'B}{D'C}=\dfrac{D'B}{D'J}.\dfrac{D'J}{D'C}=\dfrac{BG}{CJ}.\dfrac{BJ}{CG}=\dfrac{BG}{CG}.\dfrac{BJ}{CJ}\).
Mặt khác do O, T là điểm chính giữa của (BOC) nên JT là phân giác của góc BJC, GO là phân giác của góc BGC. Suy ra \(\dfrac{BG}{CG}=\dfrac{BI}{CI};\dfrac{BJ}{CJ}=\dfrac{BH}{CH}\).
Do đó \(\dfrac{D'B}{D'C}=\dfrac{BG}{CG}.\dfrac{BJ}{CJ}=\dfrac{BI}{CI}.\dfrac{BH}{CH}\).
Lại có AH, AI đẳng giác trong tam giác ABC nên \(\dfrac{BI}{CI}.\dfrac{BH}{CH}=\dfrac{AB^2}{AC^2}\Rightarrow\dfrac{D'B}{D'C}=\dfrac{AB^2}{AC^2}\)
\(\Rightarrow\) AD' là đường đối trung của tam giác ABC.
Mặt khác ta có kết quả quen thuộc AT là đường đối trung của tam giác ABC, do đó \(D'\equiv D\).
Vậy SO, TH, DG đồng quy tại J.
T
23 tháng 1 2021
Gõ lại lần cuối, không được nữa nghỉ chơi hoc24:v
Bất đẳng thức cần chứng minh tương đương với $$a^3b^2+b^3c^2+c^3a^2\geq abc(a^2+b^2+c^2)$$Ta có$2\left( {{a^3}{b^2} + {b^3}{c^2} + {c^3}{a^2}} \right) - 2abc\left( {{a^2} + {b^2} + {c^2}} \right)$$= \displaystyle\LARGE{\sum} {{a^3}} \left( {{b^2} - 2bc + {c^2}} \right) -\displaystyle \LARGE{\sum} {{a^2}} ({b^3} - {c^3})$Mặt khác ta có đẳng thức sau
$${a^2}\left( {{b^3} - {c^3}} \right) + {b^2}\left( {{c^3} - {a^3}} \right) + {c^2}\left( {{a^3} - {b^3}} \right) = {a^2}{\left( {b - c} \right)^2} + {b^2}{\left( {c - a} \right)^2} + {c^2}{\left( {a - b} \right)^2}$$Từ đó dễ dàng thu được$$2\left( {{a^3}{b^2} + {b^3}{c^2} + {c^3}{a^2}} \right) - 2abc\left( {{a^2} + {b^2} + {c^2}} \right)$$$$= {a^2}{\left( {b - c} \right)^2}\left( {a - b + c} \right) + {b^2}{\left( {c - a} \right)^2}\left( {b - c + a} \right) + {c^2}{(a - b)^2}\left( {c - a + b} \right)$$$$= {S_a}{\left( {b - c} \right)^2} + {S_b}{\left( {c - a} \right)^2} + {S_c}{\left( {a - b} \right)^2}$$Với $${S_a} = {a^2}\left( {a - b + c} \right)$$$${S_b} = {b^2}\left( {b - c + a} \right)$$$${S_c} = {c^2}\left( {c - a + b} \right)$$Do $a,$$b,$$c$ là độ dài ba cạnh tam giác nên rõ ràng $S_a,S_b,S_c$ không âm. Ta thu được điều hiển nhiên.
T
27 tháng 1 2021
Xét hiệu hai vế bất đẳng thức đã cho ta được:
\(VT-VP={\dfrac { \left( a-b \right) ^{2}{c}^{2}}{ \left( b+c \right) \left( c +a \right) \left( a+b+c \right) }}+{\dfrac { \left( b-c \right) ^{2}{a }^{2}}{ \left( a+b \right) \left( c+a \right) \left( a+b+c \right) } }+{\dfrac { \left( ac-{b}^{2} \right) ^{2}}{ \left( a+b \right) \left( b+c \right) \left( a+b+c \right) }}\geqslant 0. \)
Đẳng thức xảy ra khi $a=b=c.$
T
27 tháng 1 2021
Cách khác.
Quy đồng, ta cần chứng minh:
\(2\,{a}^{3}{c}^{2}+{a}^{2}{b}^{3}-3\,{a}^{2}{b}^{2}c-2\,{a}^{2}b{c}^{2} +2\,{a}^{2}{c}^{3}+a{b}^{4}-3\,a{b}^{2}{c}^{2}+{b}^{4}c+{b}^{3}{c}^{2}\geq 0\)
Sử dụng bất đẳng thức AM-GM, ta có:
\(3\,a{b}^{2}{c}^{2}\leq \dfrac{5}{4}{a}^{2}{c}^{3}+\dfrac{1}{2}\,a{b}^{4}+\dfrac{1}{4} \,{b}^{4}c+{b}^{3}{c}^{2},\\2\,{a}^{2}b{c}^{2}\leq {\dfrac {7\,{a}^{3}{c} ^{2}}{10}}+\dfrac{1}{5}{a}^{2}{b}^{3}+\dfrac{3}{4}{a}^{2}{c}^{3}+{\dfrac {7\,{b}^{4}c }{20}},\\3\,{a}^{2}{b}^{2}c\leq {\dfrac {13\,{a}^{3}{c}^{2}}{10}}+\dfrac{4}{5}{a }^{2}{b}^{3}+\dfrac{1}{2}a{b}^{4}+\dfrac{2}{5}{b}^{4}c \)
Xong :D
S
24 tháng 1 2021
[Toán.C35 _ 24.1.2021]
Điền hai số còn thiếu vào quy luật sau: 0 - 1 - 13 - 61 - ? - ?
\(\Rightarrow0-1-13-61-253-1017\)
[Toán.C36 _ 24.1.2021]
Điền số còn thiếu vào quy luật sau: 32 - 12 - 136 - 176 - ? - 196
\(\Rightarrow\text{32-12-136-176-186-196}\)
T
24 tháng 1 2021
Xí câu dễ trước
Câu 31.
a) Thay $b=\dfrac{5-3a}{4}$ vào và rút gọn thì cần chứng minh $(5a-3)^2\geqslant 0.$
b) Ta có: \(5^2=\left(2+3\right)\left(2a^2+3b^2\right)\ge\left(2a+3b\right)^2\Rightarrow2a+3b\le5\)
Đẳng thức xảy ra khi \(a=b=1.\)
T
24 tháng 1 2021
Bài 33.
Chuyển về pqr, cần chứng minh:
\({\dfrac { \left( {p}^{2}-3\,q \right) \left( {p}^{3}q-{p}^{2}r-2\,p{q} ^{2}+6\,qr \right) }{2qr \left( {p}^{2}-2\,q \right) }}\geqslant 0 \)
Đây là điều hiển nhiên nếu khai triển biểu thức \({p}^{3}q-{p}^{2}r-2\,p{q}^{2}+6\,qr\) ta sẽ được một đa thức với tất cả hệ số đều dương.
QT
Quoc Tran Anh Le
Giáo viên
28 tháng 12 2020
Ngoài đăng trên facebook anh cũng sẽ đăng trên hoc24 là chính. Em theo dõi những diễn biến tiếp theo của cuộc thi nha :>
Tháng 7 mới bắt đầu bạn ơi
ồ cảm ơn bạn nhaa