Phân tích đa thức thành nhân tử bằng cách tách hạng tử bậc nhất: x^2 - 11x + 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



phương pháp này mình gọi là phương pháp nhẩm nghiệm:
- Nếu tổng tất cả các hệ số bằng o thì đa thức có 1 nghiệm là x=1 hay chứa thừa số là x-1
- Nếu tổng tất cả các hệ số bậc chẵn bằng tổng các hệ số bậc lẻ thì đa thức có một nghiệm là x=-1 hay chứa thừa số là x+1

\(x^2-x-xy-2y^2+2y\)
\(=x^2-x-2xy+xy-2y^2+2y\)
\(=\left(-2y^2-2xy+2y\right)+\left(xy+x^2-x\right)\)
\(=2y\left(-y-x+1\right)-x\left(-y-x+1\right)\)
\(=\left(2y-x\right)\left(-y-x+1\right)\)

a: \(4x^2-x-5=\left(4x-5\right)\left(x+1\right)\)
b: \(x^2-2x-15=\left(x-5\right)\left(x+3\right)\)

x2-10x+16=x2-8x-2x+16=(x2-8x)-(2x-16)=x(x-8)-2(x-8)=(x-8)(x-2)
Ai có đề phân tích đa thức thành nhân tử bằng pp tách hạng tử thì cho mình xin nhé ( bậc 2 trở lên )

Bạn ơi ở câu hỏi tương tự có pp bậc ba trở lên đấy

\(3x^2+10x+3\)
\(=3x^2+x+9x+3\)
\(=x\left(3x+1\right)+3\left(3x+1\right)\)
\(=\left(3x+1\right)\left(x+3\right)\)
\(3x^2+10x+3=3x^2+9x+x+3=3x\left(x+3\right)+\left(x+3\right)\)
\(=\left(3x+1\right)\left(x+3\right)\)
chúc bn học tốt

\(12x^2+7x-12=12x^2-5x+12x-12\)
\(=x\left(12x-5\right)+12\left(x-1\right)\)
Đề sai rồi bạn ời

=yz(x^2+5x-14)
=yz(x^2-2x+7x-14)
=yz[x(x-2)+7(x-2)
=yz(x-2)(x+7)
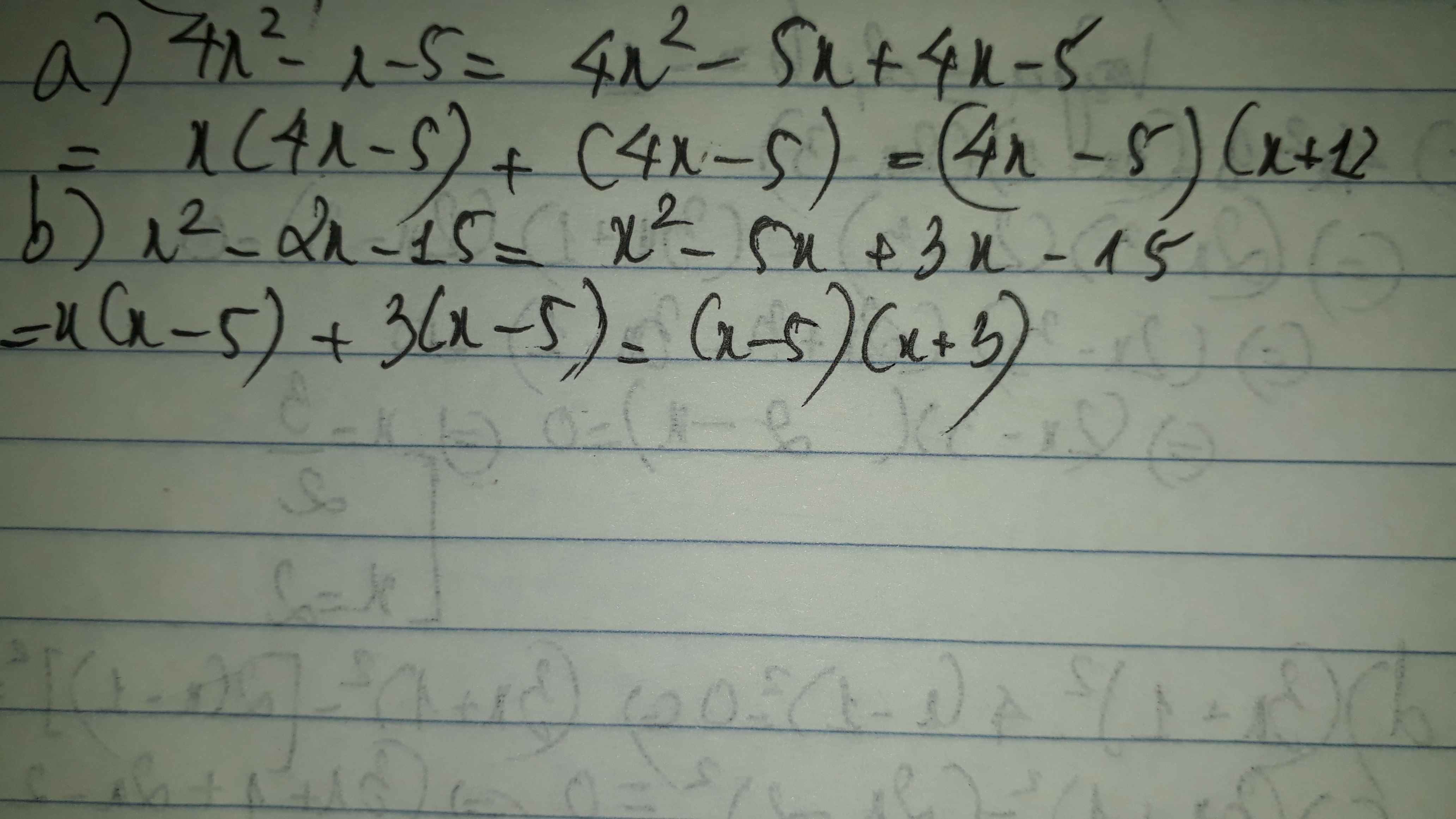
= [x2 - 2.x.\(\frac{11}{2}\) + \(\left(\frac{11}{2}\right)^2\)] - \(\frac{121}{4}\)+ 8 = (x - \(\frac{11}{2}\))2 - \(\frac{89}{4}\) = (x - \(\frac{11}{2}\))2 - \(\left(\frac{\sqrt{89}}{2}\right)^2\)
= \(\left(x-\frac{11}{2}-\frac{\sqrt{89}}{2}\right).\left(x-\frac{11}{2}+\frac{\sqrt{89}}{2}\right)\)= \(\left(x-\frac{11+\sqrt{89}}{2}\right).\left(x+\frac{\sqrt{89}-11}{2}\right)\)