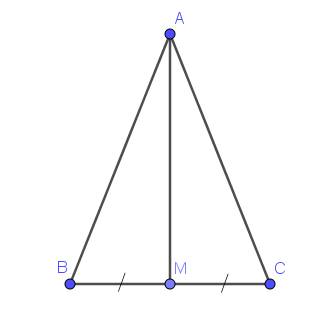
Cho tam giác ABC cân tại A . Gọi M là trung điểm của BC. Chứng minh AM vuông góc với BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Ta có: ΔABC cân tại A
mà AE là đường trung tuyến
nên AE là đường cao

a: ΔABC cân tại A
mà AM là đường cao
nên AM là trung trực của BC(1)
b: DB=DC
nên D nằm trên trung trực của BC(2)
(1), (2) =>A,M,D thẳng hàng

Lời giải:
a.
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.
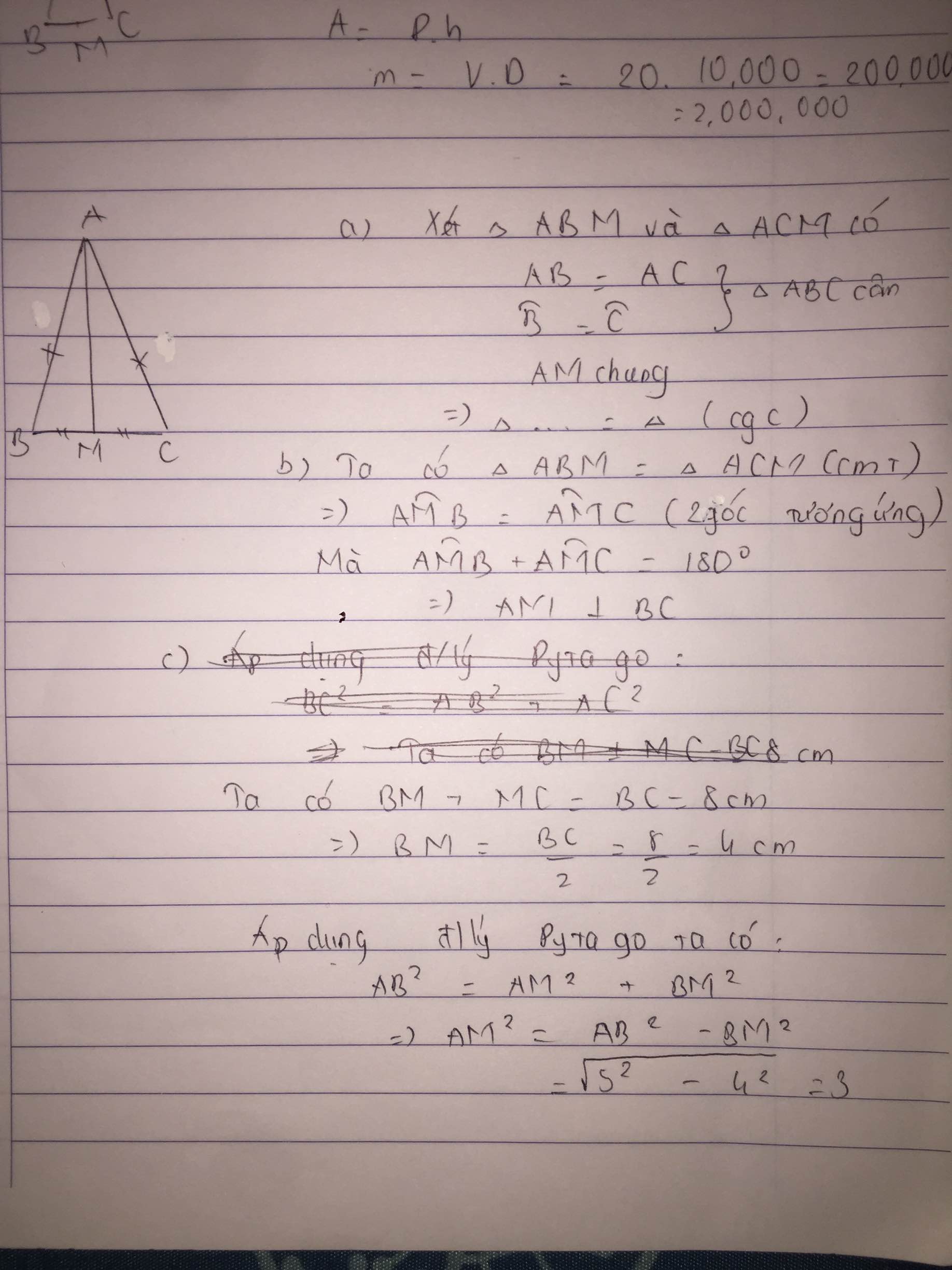

AB = AC nên A nằm trên đường trung trực của BC.
MB = MC nên M cũng vậy
Suy ra AM là trung trực của BC do đó AM vuông góc BC.
Tam giác ABC cân có M là trung điểm ==> AM là trung tuyến của tam giác ABC
Mà trong tam giác cân, đường trang tuyến là đường cao ==> AM vuông góc với BC