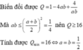Cho a>0: b≥ 0 thỏa mãn a3 + b3 = a – b. Tìm giá trị nhỏ nhất của biểu thức: M = 2017 – a3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do \(0\le a,b,c\le1\)
nên\(\left\{{}\begin{matrix}\left(a^2-1\right)\left(b-1\right)\ge0\\\left(b^2-1\right)\left(c-1\right)\ge0\\\left(c^2-1\right)\left(a-1\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b-b-a^2+1\ge0\\b^2c-c-b^2+1\ge0\\c^2a-a-c^2+1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b\ge a^2+b-1\\b^2c\ge b^2+c-1\\c^2a\ge c^2+a-1\end{matrix}\right.\)
Ta cũng có:
\(2\left(a^3+b^3+c^3\right)\le a^2+b+b^2+c+c^2+a\)
Do đó \(T=2\left(a^3+b^3+c^3\right)-\left(a^2b+b^2c+c^2a\right)\)
\(\le a^2+b+b^2+c+c^2+a\)\(-\left(a^2+b-1+b^2+c-1+c^2+a-1\right)\)
\(=3\)
Vậy GTLN của T=3, đạt được chẳng hạn khi \(a=1;b=0;c=1\)

\(a)\) Ta có :
\(M=a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)\)
Thay \(a+b=1\) vào \(M=\left(a+b\right)\left(a^2+b^2-ab\right)\) ta được :
\(M=\left(a+b\right)\left(a^2+b^2-ab\right)=1\left(a^2+b^2-ab\right)=a^2+b^2-ab\)
Lại có :
\(a^2\ge0\)
\(b^2\ge0\)
\(\Rightarrow\)\(a^2+b^2\ge0\)
\(\Rightarrow\)\(a^2+b^2-ab\ge-ab\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}a^2=0\\b^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}a=0\\b=0\end{cases}}}\)
Vậy \(M_{min}=-ab\) khi \(a=b=0\)
Sai thì thôi nhé, mk mới lớp 7
dytt me dễ vãi lone
\(a^3+\frac{1}{8}+\frac{1}{8}\ge3\sqrt[3]{\frac{a^3.1}{8.8}}=\frac{3}{4}a.\)
\(b^3+\frac{1}{8}+\frac{1}{8}\ge\frac{3}{4}b\)
\(M+\frac{4}{8}\ge\frac{3}{4}\left(a+b\right)=\frac{3}{4}\Leftrightarrow M\ge\frac{3}{4}-\frac{4}{8}=?\) tự tính dcmmm
b.
\(a^3+1+1\ge3\sqrt[3]{a^3}=3a\)
\(b^3+1+1\ge3b\)
\(a^3+b^3+4\ge3\left(A+b\right)\)
cái dmcmmm a^3+b^3=2 suy ra
\(6\ge3\left(a+b\right)\)
\(2\ge a+b\)
dytt cụ m tự kết luận

bài 5 nhé:
a) (a+1)2>=4a
<=>a2+2a+1>=4a
<=>a2-2a+1.>=0
<=>(a-1)2>=0 (luôn đúng)
vậy......
b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:
a+1>=\(2\sqrt{a}\)
tương tự ta có:
b+1>=\(2\sqrt{b}\)
c+1>=\(2\sqrt{c}\)
nhân vế với vế ta có:
(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)
<=>(a+)(b+1)(c+1)>=8 (vì abc=1)
vậy....

\(5,M=a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\\ M=\left(a+b\right)\left[\left(a+b\right)^2-3ab\right]\\ M=1\left(1-3ab\right)=1-3ab\ge1-\dfrac{3\left(a+b\right)^2}{4}=1-\dfrac{3}{4}=\dfrac{1}{4}\\ M_{min}=\dfrac{1}{4}\Leftrightarrow a=b=\dfrac{1}{2}\)

Câu 5:
\(a+b=1\Rightarrow a=1-b\)
\(M=a^3+b^3=\left(1-b\right)^3+b^3=1-3b+3b^2-b^3+b^3\)
\(=1-3b+3b^2=3\left(b^2-b+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(b-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)
\(minM=\dfrac{1}{4}\Leftrightarrow a=b=\dfrac{1}{2}\)
Câu 7:
\(a^3+b^3+abc\ge ab\left(a+b+c\right)\)
\(\Leftrightarrow a^3+b^3+abc-ab\left(a+b+c\right)\ge0\)
\(\Leftrightarrow a^3+b^3-a^2b-ab^2\ge0\)
\(\Leftrightarrow a^2\left(a-b\right)-b^2\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2-b^2\right)\ge0\Leftrightarrow\left(a-b\right)^2\left(a+b\right)\ge0\)(đúng do a,b dương)
Dấu "=" xảy ra \(\Leftrightarrow a=b\)