Cho N= n1+n2+n3+...+n99+n100=2013. Đăt S=n21+n22+n23+...+n299+n2100. Chứng tỏ rằng: (S-1)chia hết 2. Với n1;n2;n3;...;n99;n100 là các số tự nhiên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu hỏi của Dung Viet Nguyen - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại link trên nhé.


Gọi n1, n2 lần lượt là chiết suất của môi trường A và môi trường B đối với một ánh sáng đơn sắc. Chiết suất tỉ đối của môi trường A so với môi trường B là: n12=\(\dfrac{n1}{n2}\)

Vẽ Hình
b) Vì 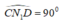 nên
nên 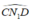 là góc nội tiếp chắn nửa đường tròn đường kính CD hay
N
1
,
nằm trên đường tròn đường kính CD
là góc nội tiếp chắn nửa đường tròn đường kính CD hay
N
1
,
nằm trên đường tròn đường kính CD
Tương tự như vậy ta chứng minh được N 2 , N 3 nằm trên đường tròn đường kính CD
Vậy N 1 , N 2 , N 3 nằm trên đường tròn đường kính CD

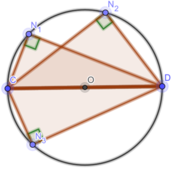
a. Q ^ 1 = 60 ° ( kề bù với Q ^ 4 ) mà Q 1 ^ đồng vị với M ^ = 60 ° => a//b
b. Vì a//b N 4 ^ = P ^ 4 = 30 ° ( đồng vị) ⇒ N ^ 1 = N ^ 3 = 150 ° ⇒ N ^ 4 = N ^ 2 = 130 °

Vì 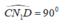 nên
nên 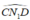 là góc nội tiếp chắn nửa đường tròn đường kính CD hay N1 nằm trên đường tròn đường kính CD
là góc nội tiếp chắn nửa đường tròn đường kính CD hay N1 nằm trên đường tròn đường kính CD
Tương tự như vậy ta chứng minh được N2,N3 nằm trên đường tròn đường kính CD
Vậy N1,N2,N3 nằm trên đường tròn đường kính CD

\(a,S=\dfrac{\left(2014+4\right)\left[\left(2014-4\right):3+1\right]}{2}=\dfrac{2018\cdot671}{2}=677039\\ b,\forall n\text{ lẻ }\Rightarrow n+2013\text{ chẵn }\Rightarrow n\left(n+2013\right)⋮2\left(1\right)\\ \forall n\text{ chẵn }\Rightarrow n\left(n+2013\right)⋮2\left(2\right)\\ \left(1\right)\left(2\right)\RightarrowĐpcm\\ c,M=\left(2+2^2+2^3+2^4\right)+...+\left(2^{17}+2^{18}+2^{19}+2^{10}\right)\\ M=2\left(1+2+2^2+2^3\right)+...+2^{16}\left(1+2+2^2+2^3\right)\\ M=\left(1+2+2^2+2^3\right)\left(2+...+2^{16}\right)=15\left(2+...+2^{16}\right)⋮15\)