cho 3 số tự nhiên a;b;c thỏa mãn a2+b2=c2chứng tỏ rằng abc chia hết cho 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a bằng giá trị trung bình cộng của 7,11 và a. Vì vậy a có giá trị bằng trung bình cộng của 7 và 11.
Số tự nhiên a cần tìm là:
(7+11):2=9
Đáp số: a là 9

Giải toán bằng sơ đồ đoạn thẳng của tiểu học em nhé
Tổng của hai số 7 và 11 là: 7 + 11 = 18
Coi trung bình cộng của ba số là 1 phần ta có sơ đồ
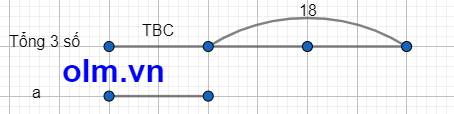
theo sơ đồ ta có:
Số tự nhiên a là: 18 : 2 = 9
Đáp số: 9

a là BCNN của 3/5 và 10/7 tức là a(BCNN) của 5 và 10
a = 10

Khi bớt số tự nhiên \(a\)ở tử và thêm ở mẫu thì tổng của tử số và mẫu số không đổi.
Tổng của tử số và mẫu số là:
\(23+17=40\)
Nếu phân số mới có tử số là \(2\)phần thì mẫu số là \(3\)phần.
Tổng số phần bằng nhau là:
\(2+3=5\)(phần)
Tử số mới là:
\(40\div5\times2=16\)
Số tự nhiên \(a\)là:
\(23-16=7\)

a chia 3/5 thuộc N=)3a chia hết cho 5=)30a chia hết cho 50
a chia 10/7 thuộc N=)10a chia hết cho 7=)30a chia hết cho 21
=)30a chia hết cho BCNN(50,21)
=)30a chia hết cho 1050
=)a chia hết cho 350
mà a nhỏ nhất =)a=350

Bài 1
a) 102
b)108
Bài 2
a) Gọi số cần tìm là a;a+1;a+2
Ta có: a+a+1+a+1=3a+3
Vi 3chia hết cho 3=>3a sẽ chia hết cho 3
=3a+3 chia hết cho 3
=>tổng của 3 số tự nhiên liên tiếp sẽ chia hết cho 3

1: A) Số đó là: 102
B) Số đó là 108
2: A). Gọi 3 số đó là a; a + 1; a + 2
Ta có: a + a + 1 + a + 2 = 3a +3
3 chia hết cho 3 => 3a chia hết cho 3
=> 3a + 3 chia hết cho 3
=> Tổng của 3 số tự nhiên liên tiếp luôn chia hết cho 3
B) Mình chịu vì mình không biết làm. Xin lỗi bạn
~ Chúc bạn học tốt ~
1
a) 102
b ) 108
2
a) ví dụ
1+2+3=6'
4+5+6=15
6+7+8=21
b)
1x2x3=6
2 x 3 x 4 = 24
3 x 4 x 5 =60
nhớ k cho mình nha

b.Gọi số cần tìm là a.
Ta có: a : 3 dư 1 \(\Rightarrow\) a + 2 \(⋮\) 3
a : 5 dư 3 \(\Rightarrow\) a + 2 \(⋮\) 5 và a là nhỏ nhất
a : 7 dư 5 \(\Rightarrow\) a + 2 \(⋮\) 7
\(\Rightarrow\) a + 2 \(\in\) BCNN( 3, 5, 7 ).
\(\Rightarrow\) BCNN( 3, 5, 7 ) = 3.5.7 = 105.
\(\Rightarrow\) a + 2 = 105
\(\Rightarrow\) a = 103
Bài làm thì đúng nhưng bội chung lớn nhất là sai phải là bội chung nhỏ nhất mới đúng.![]()
Giải:
Ta có: \(12=3.4\)
+) Nếu \(a,b,c\) \(⋮̸\) \(3\Rightarrow a^2,b^2,c^2\div3\) dư \(1\)
Khi đó \(a^2+b^2=BS3+2;c^2=BS3+1\) (vô lí)
\(\Rightarrow\left[{}\begin{matrix}a⋮3\\b⋮3\\c⋮3\end{matrix}\right.\)\(\Rightarrow abc⋮3\left(1\right)\)
+) Nếu \(a,b,c\) \(⋮̸\) \(4\Rightarrow a^2,b^2,c^2\div8\) dư \(1;4\)
Khi đó \(a^2+b^2\div8\) dư \(0;2;5;c^2\div5\) dư \(1;4\) (vô lí)
\(\Rightarrow\left[{}\begin{matrix}a⋮4\\b⋮4\\c⋮4\end{matrix}\right.\)\(\Rightarrow abc⋮4\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}abc⋮3\\abc⋮4\end{matrix}\right.\) Mà \(\left(3;4\right)=1\Rightarrow abc⋮12\)
Vậy nếu \(a^2+b^2=c^2\) thì \(abc⋮12\) (Đpcm)