Cho hàm số \(y=f\left(x\right)=ax+2\) có đồ thị đi qua điểm \(A\left(a-1;a^2+a\right)\)
a) Tìm a.
b) Vs a vừa tìm được, tìm giá trị của x thỏa mãn : \(f\left(2x-1\right)=f\left(1-2x\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(\begin{array}{l}f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}{x^2} - \frac{1}{2}}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {{x^2} - 1} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{1}{2}\left( {x + 1} \right) = \frac{1}{2}\left( {1 + 1} \right) = 1\end{array}\)
b) Phương trình đường thẳng \(d\) đi qua điểm \(M\left( {1;\frac{1}{2}} \right)\) và có hệ số góc bằng \(k = f'\left( 1 \right) = 1\) là: \(y - \frac{1}{2} = 1\left( {x - 1} \right) \Leftrightarrow y = x - 1 + \frac{1}{2} \Leftrightarrow y = x - \frac{1}{2}\).

Đường thẳng \(d\) cắt đồ thị hàm số \(\left( C \right)\) tại duy nhất điểm \(M\left( {1;\frac{1}{2}} \right)\).

a) Quan sát đồ thị:
điểm \(\left( {1; - 2} \right)\) (tức là có x =1; y=-2) thuộc đồ thị.
điểm \(\left( {2; - 1} \right)\) (tức là có x=2; y=-1) thuộc đồ thị hàm số.
điểm (0;0) không thuộc đồ thị hàm số.
b) Từ điểm trên Ox: \(x = 0\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 0 \right) = - 1\)
Từ điểm trên Ox: \(x = 3\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 3 \right) = 0\)
c) Giao điểm của đồ thị và trục Ox là điểm \(\left( {3;0} \right)\).

a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
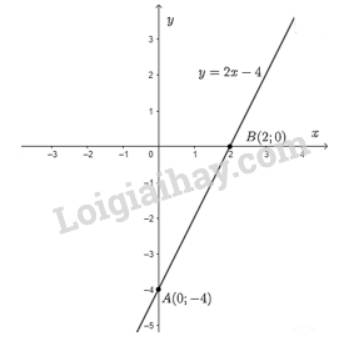
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).

- Thay \(x=a+2,y=3a^2+2a\) vào hàm số f(X) ta được :
\(3a^2+2a=a\left(a+2\right)+\frac{8}{9}\)
=> \(3a^2+2a=a^2+2a+\frac{8}{9}\)
=> \(3a^2+2a-a^2-2a-\frac{8}{9}=0\)
=> \(2a^2-\frac{8}{9}=0\)
=> \(a^2=\frac{4}{9}\)
=> \(\orbr{\begin{cases}a=-\frac{2}{3}\\a=\frac{2}{3}\end{cases}}\)
Vậy a có các giá trị là \(a=-\frac{2}{3},a=\frac{2}{3}\)

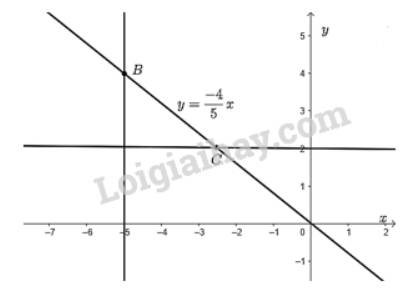
Từ điểm \(y = 2\) trên \(Oy\) vẽ đường thẳng vuông góc với \(Oy\) cắt đồ thị hàm số tại điểm \(C\). Khi đó, điểm \(C\) là điểm trên đồ thị hàm số có tung độ bằng 2.

Bài 1:
a: Thay x=-2 và y=2 vào hàm số, ta được:
4a=2
hay a=1/2
Bài 2:
a: \(\Leftrightarrow\left\{{}\begin{matrix}4x+5y=3\\4x-12y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}17y=-17\\x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\3y=x-5=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}=1\\\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{y}=\dfrac{1}{2}-\dfrac{1}{5}=\dfrac{3}{10}\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(2;\dfrac{10}{3}\right)\)

a, gọi điểm hàm số (1) luôn đi qua là A(xo,yo) thì xo,yo thỏa mãn (1)
\(=>yo=\left(a-1\right)xo+a< ->a.\left(xo+1\right)-\left(xo+yo\right)=0\)
\(=>\left\{{}\begin{matrix}xo+1=0\\xo+yo=0\end{matrix}\right.\)=>xo=-1,yo=1 vậy.....
b,\(=>x=0,y=3=>\left(1\right):a=3\)(tm)
c,\(=>x=-2,y=0=>\left(1\right):0=\left(a-1\right)\left(-2\right)+a=>a=2\left(tm\right)\)
\(=>y=x+2\) cho x=0=>y=2=>A(0;2)
cho y=0=>x=-2=>B(-2;0)
gọi OH là khoảng cách từ gốc tọa độ đến đồ thị hàm số(1)
\(=>\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=>\dfrac{1}{OH^2}=\dfrac{1}{2^2}+\dfrac{1}{\left(-2\right)^2}=>OH=....\)
Giải:
Vì đồ thị hàm số \(y=f\left(x\right)=ax+2\) đi qua điểm \(A\left(a-1;a^2+a\right)\) nên:
\(a^2+a=a\left(a-1\right)+2\)
\(\Leftrightarrow a^2+a=a^2-a+2\)
\(\Leftrightarrow2a=2\Leftrightarrow a=\dfrac{2}{2}=1\)
b) Với \(a=1\) thì \(y=f\left(x\right)=x+2\) ta có:
\(f\left(2x-1\right)=f\left(1-2x\right)\)
\(\Leftrightarrow\left(2x-1\right)+2=\left(1-2x\right)+2\)
\(\Leftrightarrow4x=2\Leftrightarrow x=\dfrac{2}{4}=\dfrac{1}{2}\)