Cho 3 điện trở \(R_1=10\Omega;R_2=15\Omega;R_3=5\Omega\) . Có thể mắc 3 điện trở này thành các mạch điện như thế nào để khi đặt vào 2 đầu đoạn mạch 1 hiệu điện thế \(U=12V\) thì \(I=0,8A\) ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 11 2021
\(R_{tđ}=R_1+R_2+R_3=1+2+2=5\Omega\)
\(I_1=I_2=I_3=I=\dfrac{U}{R}=\dfrac{16}{5}=3,2A\)
\(U_1=I_1\cdot R_1=1\cdot3,2=3,2V\)
\(U_2=U_3=3,2\cdot2=6,4V\)
BP
29 tháng 10 2016
câu 1. 5Ω
câu 2. 9Ω
câu 3. 8Ω
câu 4. điện trở của dây dẫn càng lớn thì dòng điện đi qua nó càng nhỏ
câu 5. 30Ω và 90Ω
câu 6. 10V
câu 7. 2A
câu 8. I1=1.5I2
câu 9. \(\frac{1}{3}\)
câu 10. S1.R1=S2.R2
23 tháng 7 2018
Tóm tắt:
\(R_1ntR_2\)
\(R_1=3\Omega\)
\(R_2=5\Omega\)
\(U=12V\)
\(I_1=?\)
\(I_2=?\)
-----------------------------------------
Bài làm:
Điện trở tương đương của đoạn mạch là:
\(R_{TĐ}=R_1+R_2=3+5=8\left(\Omega\right)\)
Cường độ dòng điện chạy qua đoạn mạch là:
\(I=\dfrac{U}{R_{TĐ}}=\dfrac{12}{9}=\dfrac{4}{3}\approx1,33\left(A\right)\)
Vì \(R_1ntR_2\) nên: \(I_1=I_2=I=1,33\left(A\right)\)
Vậy ...................................
23 tháng 5 2022
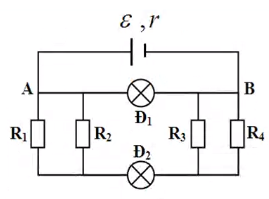
a, Cường độ tương đương của mạch:
\(R_{tđ}=R_1+R_2=40\Omega\)
Cường độ dòng điện qua mỗi điện trở:
\(I=\dfrac{U}{R_1+R_2}=\dfrac{12}{25+15}=0,3A\)
b, Đổi \(S=0,06mm^2=0,06.10^{-6}m^2\)
Công thức tính điện trở:
\(R=\rho\dfrac{\iota}{S}\Rightarrow l=\dfrac{RS}{\rho}\)
Thay số vào: \(\left(15.0,06.10^{-6}\right)/0,5.10^{-6}=\dfrac{9}{5}=1.8m\)
23 tháng 5 2022
a)Điện trở tương đương trong mạch: \(R=R_1+R_2=25+15=40\Omega\)
Dòng điện qua mạch: \(I=\dfrac{U}{R}=\dfrac{12}{40}=0,3A\)
Hai điện trở mắc nối tiếp\(\Rightarrow I_{R1}=I_{R2}=I_{mạch}=0,3A\)
b)Chiều dài dây dẫn:
\(R=\rho\dfrac{l}{S}\Rightarrow l=\dfrac{R\cdot S}{\rho}=\dfrac{15\cdot0,06\cdot10^{-6}}{0,5\cdot10^{-6}}=1,8m\)
23 tháng 5 2022
Điện trở tương đương của đoạn mạch AB:
\(R_{tđ}=R_1+R_2=12+36=48\left(\Omega\right)\)
Cường độ dòng điện trong mạch AB:
\(I=\dfrac{U}{R_{tđ}}=\dfrac{12}{48}=0,25\left(A\right)\)
N
11 tháng 11 2021
a. \(R_b=p_b\dfrac{l_b}{S_b}=0,5\cdot10^{-6}\dfrac{100}{3\cdot10^{-6}}=\dfrac{50}{3}\Omega\)
\(\Rightarrow I=I1=I_b=U:R=40:\left(20+\dfrac{50}{3}\right)=\dfrac{12}{11}A\left(R1ntR_b\right)\)
b. \(P_b=U_b\cdot I_b=I_b^2\cdot R_b=\left(\dfrac{12}{11}\right)^2\cdot\dfrac{50}{3}\approx19,8\)W
\(A=UIt=40\cdot\dfrac{12}{11}\cdot5\cdot60\approx13090,9\left(J\right)\)
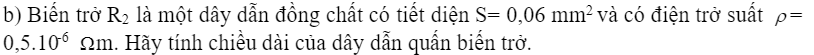
Điện trở tương đương: \(R=\dfrac{U}{I}=\dfrac{12}{0,8}=15\Omega\)
Nhận xét: Do \(R=R_2>R_1>R_3\) nên để được điện trở tương đương là \(15\Omega\) thì ta có 2 trường hợp.
+ TH1: \(R_1\) nối tiếp với (\(R_2\) song song với \(R_3\)) --> Được điện trở tương đương là \(15\Omega\), thỏa mãn.
+ TH2: \(R_3\) nối tiếp với (\(R_1\) song song với \(R_2\)) --> Điện trở tương đương là \(11\Omega\), không thỏa mãn.
Vậy có 1 cách mắc như ở trường hợp 1.