TÌM TÍCH ; M= \(\frac{1^4+4}{3^4+4}\)x \(\frac{5^4+4}{7^4+4}\)x \(\frac{9^4+4}{11^4+4}\)... \(\frac{17^4+4}{19^4+4}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) Gọi 3 số tự nhiên liên tiếp là: a, a+1, a+2 \(\left(a\in N\right)\)
Theo bài ra ta có: \(a\left(a+1\right)\left(a+2\right)=2184\)
\(\Leftrightarrow\)\(a\left(a+1\right)\left(a+2\right)-2184=0\)
\(\Leftrightarrow\)\(\left(a-12\right)\left(a^2+15a+182\right)=0\)
\(\Leftrightarrow\)\(a=12\)
Vậy 3 số tự nhiên liên tiếp đó là: 12, 13, 14

a: Gọi hai só cần tìm là a,a+1
Theo đề, ta có: a(a+1)=630
\(\Leftrightarrow a^2+a-630=0\)
\(\Delta=1^2-4\cdot1\cdot\left(-630\right)=2521\)
=>Không có hai số tự nhiên liên tiếp nào thỏa mãn đề bài
b: Gọi ba số tự nhiên liên tiếp là a;a+1;a+2
Theo đề, ta có:
\(a^3+3a^2+2a-2184=0\)
\(\Leftrightarrow a^3-12a^2+15a^2-180a+182a-2184=0\)
=>a=12
Vậy: Ba số cần tìm là 12;13;14
c: Gọi hai số liên tiếp là a,a+1
Theo đề,ta có: a(a+1)=756
\(\Leftrightarrow a^2+a-756=0\)
\(\Delta=1^2+4\cdot1\cdot756=3025\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}a_1=\dfrac{-1-55}{2}=-\dfrac{56}{2}=-28\left(loại\right)\\a_2=\dfrac{-1+55}{2}=27\left(nhận\right)\end{matrix}\right.\)
Vậy: Hai số cần tìm là 27 và 28

Do quên đánh dấu phẩy nên thừa số thứ nhất đã nhân với 45.
=> Tích tăng lên số lần là:
45 - 4,5 = 40,5 ( lần )
=> Thừa số 1 là:
1296 : 40,5 = 32
Tích đúng là:
32 x 4,5 = 144
Chúc bạn may mắn! À mà bạn ơi, k mình thêm 2 cái nữa ở trong phần thống kê hỏi đáp nhé!

Ta có (x*106)-(x*7)=45144
(106-7)*x=45144
99*x=45144
=>X=456
Suy ra tích đúng là : 456*106=48336

a) Gọi 2 số tự nhiên liên tiếp đó là: \(n,n+1\left(n\in N\right)\)
\(\Rightarrow n\left(n+1\right)=650\)
\(\Rightarrow n^2+n-650=0\)
\(\Rightarrow\left(n+\dfrac{1}{2}\right)^2=\dfrac{2601}{4}\)
\(\Rightarrow n+\dfrac{1}{2}=\dfrac{51}{2}\)
\(\Rightarrow n=25\)
Vậy 2 số đó là 25,26

câu 1 lấy tử chia mẫu
câu 2
tích= thửa số nhân thừa số
thương bằng số bi chia chia số chia

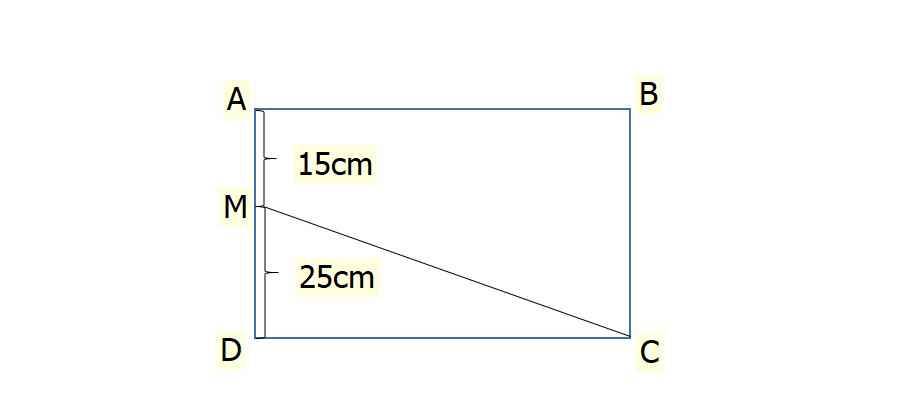
a, Độ dài CD:
(1500 x 2): 25 = 120(cm)
Độ dài AD:
15+24=40(cm)
Diện tích HCN ABCD:
40 x 120 = 4800(cm2)
b, Diện tích tứ giác AMCB:
4800 - 1500 = 3300 (cm2)
Đ.số: a,4800cm2
b, 3300cm2
Ta có : \(n^4+4=\left[\left(n-1\right)^2+1\right]\left[\left(n+1\right)^2+1\right]\)
Do đó :
\(M=\frac{1\left(2^2+1\right)}{\left(2^2+1\right)\left(4^2+1\right)}.\frac{\left(4^2+1\right)\left(6^2+1\right)}{\left(6^2+1\right)\left(8^2+1\right)}.\frac{\left(8^2+1\right)\left(10^2+1\right)}{\left(10^2+1\right)\left(12^2+1\right)}...\frac{\left(16^2+1\right)\left(18^2+1\right)}{\left(18^2+1\right)\left(20^2+1\right)}\)
\(M=\frac{1}{20^2+1}=\frac{1}{401}\)