cho hình bình hànhABCD có 2 đường chéo AC và BD cắt nhau tại O .Gọi E;F lần lượt là trung điểm của OD và OB
a) cm tứ giác AECF là hình bình hành
b)tia AE cắt CD tại P tia CF cắt AB tại Q CM AP=CQ
c)cm 3điểm P,O,Q thẳng hàng
d) cm DP=1/3DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 8 2018
Theo chứng minh ở câu a. △ AEB đồng dạng △ ABC theo tỉ số k = 1/2 nên dễ thấy BE = 1/2 BC hay BE = BM
Suy ra: ΔBEM cân tại B.
Xét tam giác EBC có: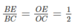 
Suy ra: OB là đường phân giác góc EBC
BO là đường phân giác góc ở đỉnh của tam giác cân BEM nên BO vuông góc với cạnh đáy EM (đpcm).
6 tháng 5 2021
Từ (1) ⇒AB⇒AB // CD ⇒⇒ AB // ND
⇒ˆA2=ˆN1⇒A2^=N1^ (5)
Từ (1) ⇒ˆABC=ˆCDA⇒ABC^=CDA^ (2 góc đối của hình bình hành) (6)
Từ (5), (6) ⇒ΔAMB∼ΔAND⇒ΔAMB∼ΔAND (G-G)
30 tháng 10 2021
a: Xét ΔAEB và ΔCFD có
AE=CF
\(\widehat{EAB}=\widehat{FCD}\)
AB=CD
Do đó: ΔAEB=ΔCFD
Suy ra:BE=FD
Xét ΔADE và ΔCBF có
AE=CF
\(\widehat{DAE}=\widehat{BCF}\)
AE=CF
Do đó: ΔADE=ΔCBF
Suy ra: DE=BF
Xét tứ giác BEDF có
BE=DF
DE=BF
Do đó: BEDF là hình bình hành