Cho tam giác ABC cân tại A có đường trung tuyến AM.Gọi H là hình chiếu vuông góc của M trên AB.Biết AB=AC=34cm;BC=32cm.Tính độ dài các đoạn MH;HA và HB?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là giao của EF và AH, K là giao AM và EF
Vì \(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\) nên AEHF là hcn
Do đó \(OE=OF=OH=OA\)
\(\Rightarrow\Delta AOF\) cân tại O \(\Rightarrow\widehat{AFO}=\widehat{FAO}\left(1\right)\)
Vì AM là trung tuyến ứng với cạnh huyền BC nên \(AM=BM=CM=\dfrac{1}{2}BC\)
\(\Rightarrow\Delta AMC\) cân tại M \(\Rightarrow\widehat{MCA}=\widehat{MAC}\left(2\right)\)
Vì tam giác AHC vuông tại H nên \(\widehat{MCA}+\widehat{FAO}=90^0\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\widehat{MAC}+\widehat{AFO}=90^0\)
Mà \(\widehat{AFO}+\widehat{MAC}+\widehat{AKF}=180^0\Rightarrow\widehat{AKF}=90^0\)
Vậy AM vuông góc EF

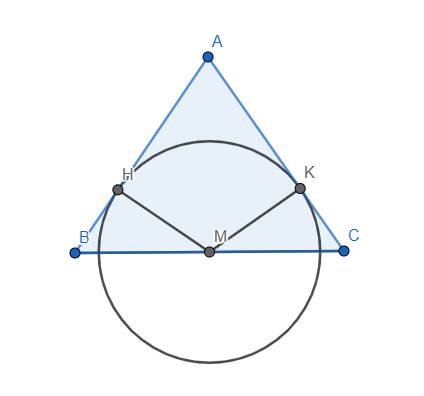
Gọi K là hình chiếu của M lên AC. Xét tam giác MBH vuông tại H và MCK vuông tại K, ta có:
\(MB=MC\) (M là trung điểm BC); \(\widehat{B}=\widehat{C}\) (tam giác ABC cân tại A)
\(\Rightarrow\Delta MBH=\Delta MCK\left(ch-gn\right)\) \(\Rightarrow MH=MK\)
Ta thấy MK chính là khoảng cách từ AC đến M, đồng thời MK bằng MH là bán kính của đường tròn (M; MH) nên AC tiếp xúc với (M) (đpcm)

a, xét tứ giác ADME có:
góc DAC = góc MDA=góc MEA=90\(^o\)
=> ADME là hình chữ nhật
b, DE=AM=5cm
c, xét tứ giác AMBH có:
BA vuông góc HM( MDA=90\(^o\))
=> AMBH là hình thoi
xét tam giác HMK có đường t/b DK(DM=DH,EK=EM)
=>DE=\(\dfrac{1}{2}HK\)
\(\Leftrightarrow DE=HA=AK\)
=> A là trung điểm HK(HA=HK)