Cho tam giác cân ABC có AB=AC . Hai đường trung trực của hai cạnh AB;AC
cắt nhau tại O . Chứng minh AOB=AOC .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



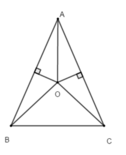
+ Vì O thuộc đường trung trực của AB nên OA = OB, do đó đáp án A sai
+ Vì ba đường trung trực của tam giác đồng quy tại một điểm nên O là giao điểm của ba đường trung trực của tam giác ABC, suy ra O thuộc đường trung trực cạnh BC
Mà AB = AC nên A thuộc đường trung trực cạnh BC
Do đó AO là đường trung trực của BC ⇒ A O ⊥ B C , nên đáp án C đúng
+ Lại có tam giác ABC cân tại A (AB = AC) có AO là trung trực nên AO cũng là phân giác của góc BAC ⇒ B A O ^ = C A O ^
Khi đó Δ B A O = Δ C A O ( c – g – c) (vì AB = AC, AO chung, B A O ^ = C A O ^ )
Suy ra A O B ^ = A O C ^ ⇒ Đáp án B sai
+ Do tam giác ABC là tam giác cân không đều nên O không phải là giao điểm của ba đường phân giác trong tam giác ABC nên O không cách đều ba cạnh của tam giác ABC, do đó đáp án D sai.
Chọn đáp án C

Vì O thuộc đường trung trực của cạnh AB nên OA = OB. Vì ba đường trung trực của một tam giác đồng quy và do tam giác ABC cân tại A nên OA là đường trung trực của BC, do đó AO ⊥ BC. Vì tam giác ABC cân tại A nên đường trung trực AO đồng thời là đường phân giác của góc A
+) Xét ΔAOB và ΔAOC có:
OA chung
AB = AC (do tam giác ABC cân tại A)
∠OAB = ∠OAC ( Do AO là tia phân giác của góc BAC)
Do đó ΔAOB = ΔAOC ( c.g.c) suy ra ∠(AOB) = ∠(AOC) .
Do tam giác ABC cân tại A nhưng không là tam giác đều nên O không là giao điểm của ba đường phân giác của tam giác ABC. Vậy O không cách đều ba cạnh của tam giác ABC.
Đáp số (C) AO ⊥ BC.

Lời giải:
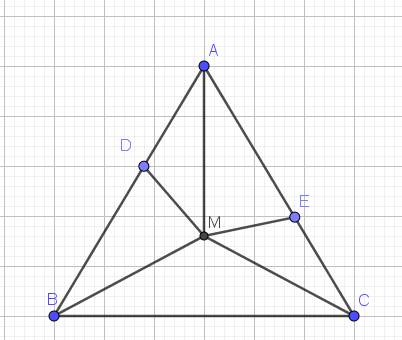
Vì $M$ nằm trên trung trực của $BC$ nên $MB=MC$. $M$ nằm trên đường trung trực của $AB$ nên $MA=MB$
$\Rightarrow MA=MB=MC$
Xét tam giác $AMC$ và $AMB$ có:
$AM$ chung
$AC=AB$ (do $ABC$ là tam giác cân tại $A$)
$MB=MC$
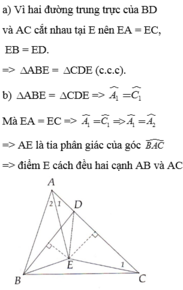
$\Rightarrow \triangle AMC=\triangle AMB$ (c.c.c)
$\Rightarrow \widehat{ACM}=\widehat{ABM}$
Hay $\widehat{ECM}=\widehat{ABM}$
Mà $\widehat{ABM}=\widehat{MAB}$ (do tam giác $MAB$ cân tại $M$ vì $MA=MB$)
$\Rightarrow \widehat{ECM}=\widehat{MAB}=\widehat{DAM}$
Xét tam giác $ECM$ và $DAM$ có:
$EC=DA$ (gt)
$\widehat{ECM}=\widehat{DAM}$ (cmt)
$CM=AM$ (cmt)
$\Rightarrow \triangle ECM=\triangle DAM$ (c.g.c)
$\Rightarrow ME=MD$ (đpcm)

Xét đường tròn (O) có: AM và AN là 2 tiếp tuyến cắt nhau tại A (gt)
\(\Rightarrow\) AM = AN (t/c 2 tiếp tuyến cắt nhau)
Mà AM = \(\dfrac{1}{2}\)AC; AN = \(\dfrac{1}{2}\)AB
\(\Rightarrow\) AB = AC
Xét tam giác ABC có: AB = AC (cmt)
\(\Rightarrow\) tam giác ABC cân tại A (đ/lí tam giác cân)
Chúc bn học tốt!

Bạn tự vẽ hình nhé. Mình giải thôi.
1)Bạn chia 2 TH.
a) Góc MDB lớn hơn hoac bằng 60 độ
=>MD<MB mà ME>MC=MB
=>MD<ME.
b) Góc MDB nhỏ hơn 60 độ.
=> MD giao CA tại E .
Dễ dàng cminh DM<ME.
2) Ta có tam giác ABC cân tại A => AI là phân giác cũng là trung trực BC
=> AI trung trực BC. Mà AO là trung trục BC.
=> AI trùng AO.
=>OI là trung trực BC
Đè bài cần xem lại nhé.
3)Ta có góc B > góc C => AC>AB
Có AC đối dienj góc vuông trong tam giác vuông AEC => AC>CE
Tương tự AB>BD
Tất cả các điều => AC-AB>CE-BD