Điền vào bảng mọi số nguyên tố mà binh phương của nó không vượt quá a, tức là p2 <;=
| a | 29 | 67 | 49 | 127 | 173 | 253 |
| b |
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta nhớ lại một số kết quả ở bài tập 57:
22 = 4; 32 = 9; 52 = 25; 72 = 49; 112 = 121; 132 = 169; 172 = 289.
Do đó ta có bảng sau:
| a | 29 | 67 | 49 | 127 | 173 | 253 |
| p | 2, 3, 5 | 2, 3, 5, 7 | 2, 3, 5, 7 | 2, 3, 5, 7, 11 | 2, 3, 5, 7, 11, 13 | 2, 3, 5, 7, 11, 13 |

a 29 67 49 127 173 253 p 2,3,5 2,3,5,7 2,3,5,7 2,3,5,7,11 2,3,5,7,11 2,3,5,7,11,13

Ta có: 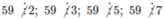
72 = 49 < 59, 112 = 121 ≥ 59
Vậy 59 là số nguyên tố
Ta có: 121 /⋮ 2; 121 /⋮ 3; 121 /⋮ 5; 121 /⋮ 7; 121 ⋮ 11
Vậy 121 là hợp số
Tương tự ta có 179; 197 và 217 là các số nguyên tố

| a | 29 | 67 | 49 | 127 | 173 | 253 |
| p | 2;3;5 | 2;3;5;7 | 2;3;5;7 | 2;3;5;7;11 | 2;3;5;7;11;13 | 2;3;5;7;11;13 |

67:2,3,5,7
49:2,3,5,7
127=2,3,5,7,11
173=2,3,5,7,11,13
253:2,3,5,7,11,13,17

| a | 59 | 121 | 179 | 197 | 217 |
| p | 2;3;5;7 | 2;3;5;7;11 | 2;3;5;7;11;13 | 2;3;5;7;11;13 | 2;3;5;7;11;13 |
tisck chominhf nha