Cho tam giác ABC đỉnh B(3;5) đường cao AH: 2x-5y+3=0, trung tuyến kẻ từ C có pt: x+y-5=0
Tính tọa độ A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C
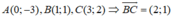
Đường cao kẻ từ A của tam giác ABC là đường thẳng đi qua A và nhận vecto BC là vecto pháp tuyến
⇒ d: 2(x - 0) + (y + 3) = 0 ⇔ 2x + y + 3 = 0

A B C M N E H
goi B(a; b) N( c; d)
\(N\in\left(CN\right)\Rightarrow\)c+8d-7 = 0(1)
N la trung diem AB\(\Rightarrow2c=1+a\left(2\right)\)
2d = -3 +b (3)
B\(\in\left(BM\right)\)\(\Rightarrow\)a+b -2 =0 (4)
tu (1) (2) (3) (4) \(\Rightarrow a=-5;b=7\Rightarrow B\left(-5;7\right)\)
dt (AE) qua vuong goc BM. \(\Rightarrow pt\)(AE):x-y-4 = 0
tọa độ H \(\left\{{}\begin{matrix}x-y-4=0\\x+y-2=0\end{matrix}\right.\Rightarrow H\left(3;-1\right)\);H là trung điểm AE
\(\Rightarrow E\left(5;1\right)\). vì ptdt (BE) cung la ptdt qua (BC):
3x+5y-20 =0
tọa độ C là nghiệm hệ \(\left\{{}\begin{matrix}3x+5y-20=0\\x+8y-7=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\dfrac{139}{21}\\\dfrac{1}{21}\end{matrix}\right.\)
\(\Rightarrow C\left(\dfrac{139}{21};\dfrac{1}{21}\right)\)

a: Đặt số đo góc A là x
Số đo góc B là y
Số đo góc C là z
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{180}{9}=20\)
Do đó: x=40; y=60; z=80

a: Xét ΔABC có AB>AC
nên \(\widehat{B}< \widehat{C}\)
b: Vì \(\widehat{B}< \widehat{C}\)
nên góc ngoài tại đỉnh B lớn hơn góc ngoài tại đỉnhC
Vì \(C\left(x_C;y_C\right)\) thuộc đồ thị hàm số \(x+y-5=0\) nên ta có \(x_C+y_C-5=0\)
\(\Leftrightarrow y_C=-x_C+5\Rightarrow C\left(x_C;-x_C+5\right)\)
phương trình đường thẳng BC có dạng \(y=ax+b\)
Vì đths \(y=ax+b\) vuông góc vs đths \(2x-5y+3=0\) nên ta có \(a.\dfrac{2}{5}=-1\Leftrightarrow a=\dfrac{-5}{2}\)
Vì B, C thuộc đths \(y=\dfrac{-5}{2}x+b\) nên ta có:
\(\left\{{}\begin{matrix}\dfrac{-5}{2}.3+b=5\\\dfrac{-5}{2}.x_C+b=-x_C+5\end{matrix}\right.\)
\(\Rightarrow\dfrac{-5}{2}\left(3-x_c\right)=x_c\)
\(\Rightarrow x_c=5\Rightarrow C\left(5;-10\right)\)
Vì A thuộc đths 2x-5y+3=0 nên ta có \(2x_A-5y_A+3=0\)(1)
Gọi M là trung điểm của AB, ta có \(\left\{{}\begin{matrix}x_M=\dfrac{x_A+3}{2}\\y_M=\dfrac{y_A+5}{2}\end{matrix}\right.\)\(\Rightarrow M\left(\dfrac{x_A+3}{2};\dfrac{y_A+5}{2}\right)\)
Vì \(M\left(\dfrac{x_A+3}{2};\dfrac{y_A+5}{2}\right)\) thuộc đths x+y-5=0 nên ta có\(\dfrac{x_A+3}{2}+\dfrac{y_A+5}{2}-5=0\)
\(\Leftrightarrow x_A+3+y_A+5-10=0\)
\(\Leftrightarrow x_A+y_A-2=0\)(2)
Từ (1), (2), ta có \(\left\{{}\begin{matrix}2x_A-5y_A+3=0\\x_A+y_A-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_A=1\\y_A=1\end{matrix}\right.\Rightarrow A\left(1;1\right)\)
Thank b