Trong không gian Oxyz cho hai điểm A(1;3;0), B(-3;1;4) và đường thẳng \(\Delta:\dfrac{x-2}{-1}=\dfrac{y+1}{1}=\dfrac{\text{z}-2}{3}\) . Xét khối nón (N) có đỉnh có tọa độ nguyên thuộc đường thẳng \(\Delta\) và ngoại tiếp mặt cầu đường kính AB. Khi (N) có thể tích nhỏ nhất thì mặt phẳng chứa đường tròn đáy của (N) có phương trình dạng ax+by+cz +1=0. Giá trị a+b+c bằng:
A.1
B.3
C.5
D.-6

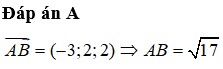
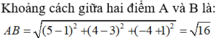
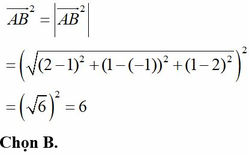
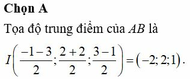

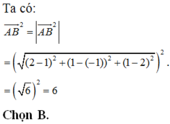

Mặt cầu tâm \(I\left(-1;2;2\right)\) bán kính \(R=3\), gọi \(r\) là bán kính đường tròn đáy và \(h\) là đường cao nón
Thực hiện mặt cắt qua trục khối nón ta được như hình bên dưới:
Đặt \(\widehat{MIH}=x\Rightarrow\widehat{NIK}=180^0-2x\)
\(r=MH=R.tanx=3tanx\)
\(IN=\dfrac{IK}{cos\left(180^0-2x\right)}=\dfrac{3}{-cos2x}\Rightarrow h=IN+IH=3-\dfrac{3}{cos2x}\)
\(V=\dfrac{1}{3}\pi R^2h=9\pi.tan^2x.\left(1-\dfrac{1}{cos2x}\right)=9\pi.tan^2x\left(1-\dfrac{1+tan^2x}{1-tan^2x}\right)\)
Đặt \(tan^2x=t>0\) và \(f\left(t\right)=t\left(1-\dfrac{1+t}{1-t}\right)=\dfrac{2t^2}{t-1}\Rightarrow f'\left(t\right)=\dfrac{2\left(t^2-2t\right)}{\left(t-1\right)^2}=0\Rightarrow t=2\)
\(f\left(t\right)_{min}=f\left(2\right)\Rightarrow V_{min}\) khi \(tan^2x=2\Rightarrow cos2x=\dfrac{1-tan^2x}{1+tan^2x}=-\dfrac{1}{3}\)
\(\Rightarrow IN=\dfrac{3}{-cos2x}=9\)
Do N thuộc \(\Delta\) nên tọa độ có dạng: \(N\left(2-t;-1+t;2+3t\right)\Rightarrow\overrightarrow{IN}=\left(3-t;t-3;3t\right)\)
\(\Rightarrow2\left(t-3\right)^2+9t^2=81\Rightarrow\left[{}\begin{matrix}t=3\\t=-\dfrac{21}{11}\left(loại\right)\end{matrix}\right.\) \(\Rightarrow N\left(-1;2;8\right)\)
Mặt phẳng (P) nhận \(\overrightarrow{IN}\) là 1 vtpt và cách I một khoảng bằng \(R=3\), bạn tự hoàn thành phần còn lại