Trong hệ trục tọa độ Oxy cho tam giác ABC có A(-1;2),B(-3;4),C(0;3). Gọi N là trung điểm của AC, M thuộc cạnh AB sao cho \(\overrightarrow{AM}=\dfrac{3}{4}\overrightarrow{AB}\). Tìm tọa độ giao điểm P của MN với BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B.
*) AH là đường cao của tam giác ABC.
*) Lập phương trình cạnh BC
B(1;-1), C(5;2) 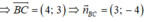
(BC): 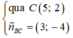
⇒ 3.(x - 5) - 4.(y - 2) = 0 ⇔ 3x - 15 - 4y + 8 = 0 ⇔ 3x - 4y - 7 = 0
Ta có:
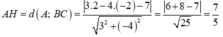

\(S=\dfrac{1}{2}\left|\left(x_B-x_A\right)\left(y_C-y_A\right)-\left(x_C-x_A\right)\left(y_B-y_A\right)\right|\)
\(=\dfrac{1}{2}\left|\left(2-1\right)\left(-8+5\right)-\left(13-1\right)\left(1+5\right)\right|=\dfrac{75}{2}\)

\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-2;3\right)\\\overrightarrow{AC}=\left(-3;5\right)\\\overrightarrow{BC}=\left(-1;2\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}AB=\sqrt{13}\\AC=\sqrt{34}\\BC=\sqrt{5}\end{matrix}\right.\)
\(cos\widehat{BAC}=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=\dfrac{21}{\sqrt{442}}\)
\(\Rightarrow\widehat{BAC}\approx2^043'\)

Phương trình đường thẳng BC: a(x-2) + b(y-2)=0
cos(BA;BC)=cos\(45^0\)=\(\dfrac{1}{\sqrt{2}}=\dfrac{\left|a-b\right|}{\sqrt{2\left(a^2+b^2\right)}}\)
\(\Leftrightarrow\left[{}\begin{matrix}a=0\\b=0\end{matrix}\right.\). Vì a,b không đồng thời bằng 0 nên suy ra \(\left[{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)
Vì tọa độ C có hoành độ x lớn hơn 2 nên phương trình đường thẳng BC là y=2.
Ta có:\(S_{ABC}=\dfrac{1}{2}AB.BC.sin45^0\)\(\Leftrightarrow2=\dfrac{1}{2}\sqrt{8}\sqrt{\left(x_C-2\right)^2}.\dfrac{\sqrt{2}}{2}\Leftrightarrow x_C=4\)
Vậy tọa độ C(4;2)

Đặt \(\overrightarrow{PB}=x\overrightarrow{BC}\)
\(\overrightarrow{PM}=\overrightarrow{PB}+\overrightarrow{BM}=x.\overrightarrow{BC}-\dfrac{1}{3}\overrightarrow{AB}\)
\(\overrightarrow{PN}=\overrightarrow{PC}+\overrightarrow{CN}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AC}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=\left(x+\dfrac{1}{2}\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AB}\)
P, M, N thẳng hàng \(\Rightarrow\dfrac{x+\dfrac{1}{2}}{x}=\dfrac{\dfrac{1}{2}}{\dfrac{1}{3}}\Rightarrow x=1\) \(\Rightarrow\overrightarrow{PB}=\overrightarrow{BC}\)
\(\Rightarrow\) B là trung điểm PC \(\Rightarrow P\left(-6;5\right)\)
Nếu bạn chưa học bài pt đường thẳng thì làm cách trên, còn học rồi thì đơn giản là thiết lập 2 pt đường thẳng BC và MN là xong