Số nghiệm thuộc đoạn[0;2017] của phương trình\(\frac{\sqrt{1+cosx}+\sqrt{1-cosx}}{sinx}=4cosx\) là:
A.1283 B.1287 C.1285 D.1284
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
PT
1
CM
7 tháng 9 2018
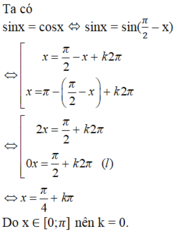
Vậy chỉ có 1 nghiệm của phương trình thuộc [0; .
Đáp án là A.
CM
16 tháng 5 2017
Đáp án B
Ta có 2 sin x − 1 = 0 ⇔ sin x = 1 2 ⇔ x = π 6 + k 2 π x = 5 π 6 + k 2 π k ∈ ℤ
Mặt khác 0 ≤ x ≤ 5 π 2 suy ra x = π 6 ; 13 π 6 ; 5 π 6 . Vậy phương trình có 3 nghiệm
PT
1
CM
22 tháng 4 2017
Ta có sin x = cos x ⇔ sin x = sin π 2 − x
⇔ x = π 2 − x + k 2 π x = π − π 2 − x + k 2 π
⇔ x = π 4 + k π , k ∈ ℤ
Do x ∈ 0 ; π nên k = 0
Vậy phương trình chỉ có một nghiệm duy nhất
ĐÁP ÁN A
CM
8 tháng 9 2018
Đáp án D
P T ⇔ cos x + 1 ≠ 0 sin 2 x = 0 ⇔ cos x ≠ − 1 2 x = k π ⇔ x ≠ π + k 2 π x = k π 2 ⇒ x = k 2 π x = π 2 + k π k ∈ ℤ .
x ∈ 2 π ; 4 π ⇒ 2 π ≤ k 2 π ≤ 4 π 2 π ≤ π 2 + k π ≤ 4 π ⇔ 1 ≤ k ≤ 2 3 2 ≤ k ≤ 7 2
Suy ra PT có 4 nghiệm thuộc đoạn 2 π ; 4 π .
CM
3 tháng 6 2018
Đáp án D
P T ⇔ m + 1 1 − c os 2 x 2 − sin 2 x + cos 2 x = 0 ⇔ sin 2 x + m − 1 2 c os 2 x = m + 1 2 .
PT có nghiệm ⇔ 1 2 + m − 1 2 2 ≥ m + 1 2 2 ⇔ m ≤ 1.
Vì m ∈ − 2018 ; 2018 ⇒ có 2020 giá trị nguyên của m.
ĐKXĐ: \(x\ne k\pi\)
\(\Leftrightarrow\sqrt{1+cosx}+\sqrt{1-cosx}=4sinx.cosx\) (\(sinx.cosx\ge0\))
\(\Leftrightarrow2+2\sqrt{sin^2x}=16sin^2x.cos^2x\)
\(\Leftrightarrow1+\sqrt{sin^2x}=8sin^2x\left(1-sin^2x\right)\)
Đặt \(\sqrt{sin^2x}=a\ge0\)
\(\Leftrightarrow1+a=8a^2\left(1-a^2\right)\)
\(\Leftrightarrow1+a=8a^2\left(1+a\right)\left(1-a\right)\)
\(\Leftrightarrow8a^2\left(1-a\right)=1\)
\(\Leftrightarrow8a^3-8a^2+1=0\)
\(\Leftrightarrow\left(2a-1\right)\left(4a^2-2a-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}a=\frac{1}{2}\\a=\frac{1+\sqrt{5}}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left|sinx\right|=\frac{1}{2}=sin\left(\frac{\pi}{6}\right)\\\left|sinx\right|=\frac{1+\sqrt{5}}{4}=sin\left(\frac{3\pi}{10}\right)\end{matrix}\right.\)
Hơi nhiều, làm biếng quá, bạn tự làm tiếp.
Lưu ý chỉ lấy các nghiệm thuộc góc phần tư thứ nhất và thứ 3