Cho hàm số y=ax2 (P) (a khác 0) đi qua điểm A(1;2)
a) xác gđịnh a và vẽ đồ thị hàm số vừa tìm dc
b) đường thẳng y= -x + b cắt (P) tại 2 điểm A và B. Xác định b và vẽ tọa độ điểm B
c) cho đường thẳng (d): y= mx - m2 - \(\dfrac{3}{2}\)m -\(\dfrac{3}{4}\). Chứng minh (d) và (P) không cắt nhau với mọi giá trị m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(P) đi qua điểm A (−2; 4) nên 4 = a. ( − 2 ) 2 = 4a a = 1
Vậy phương trình parabol (P) là y = x 2 .
Để (P) tiếp xúc với (d) thì phương trình hoành độ giao điểm
x 2 = 2 (m – 1)x – (m – 1)có nghiệm kép
↔ ∆ ’ = [ − ( m – 1 ) ] 2 − m + 1 = 0 ↔ m 2 – 2m + 1 − m + 1 = 0 ↔ m 2 – 3m + 2 = 0 ↔ m=1 hoặc m=2
Nếu m = 1 thì hoành độ giao điểm là x = 0. Vậy tiếp điểm là (0; 0)
Nếu m = 2 thì hoành độ giao điểm là x = 1. Vậy tiếp điểm là (1; 1)
Đáp án: C

a, y = ax^2 đi qua B(2;4)
<=> 4a = 4 <=> a = 1
b, bạn tự vẽ
a: Thay x=2 và y=4 vào hàm số, ta được:
\(a\cdot4=4\)
hay a=1
b: Thay x=2 và y=4 vào hàm số, ta được:
4a=4
hay a=1
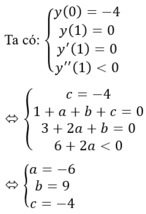

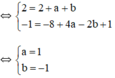
a) Thay x=1 và y=2 vào (P), ta được:
\(a\cdot1^2=2\)
hay a=2
giải hộ mình câu c dc ko :)