Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x + 2y - 2z + 2 =0 và mặt cầu tâm I(1;4;1) bán kính R tiếp xúc với (P). Bán kính R là:
A. R = 7 3
B. R = 3
C. R = 1
D. R = 9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Tiếp điểm là hình chiếu vuông góc của I lên mặt phẳng (P)

Đáp án A
Do (P) tiếp xúc với (S) nên bán kính của (S) là R = d(I, (P)) = 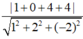 = 3. Vậy phương trình mặt cầu (S) là (x-1)² + y² + (z+2)² =9.
= 3. Vậy phương trình mặt cầu (S) là (x-1)² + y² + (z+2)² =9.

Chọn D
Phương pháp
+ Cho mặt cầu (S) có tâm I và bán kính R và mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn có bán kính r thì ta có mối liên hệ ![]() với h = d(I,(P)). Từ đó ta tính được R.
với h = d(I,(P)). Từ đó ta tính được R.
Cách giải
+ Ta có


Đáp án D
Khoảng cách từ tâm I đến mặt phẳng (P) là d(I;(P))=3
Ta có R = r 2 + d 2 = 5 2 + 3 2 = 34 với R là bán kính mặt cầu (S)
Phương trình mặt cầu là S : x + 1 2 + y - 2 2 + z + 1 2 = 34

Chọn đáp án D
Phương pháp
+ Cho mặt cầu (S) có tâm I và bán kính R và mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn có bán kính r thì ta có mối liên hệ R 2 = h 2 + r 2 với h=d(I,(P)). Từ đó ta tính được R.
+ Phương trình mặt cầu tâm I ( x 0 ; y 0 ; z 0 ) và bán kính R có dạng
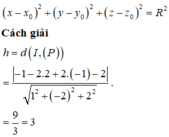
Từ đề bài ta có bán kính đường tròn giao tuyến là r=5 nên bán kính mặt cầu là
![]()
+ Phương trình mặt cầu tâm I(-1;2;-1) và bán kính R = 34 là
![]()
Đáp án B
Mặt cầu tâm I(1;4;1) tiếp xúc với mặt phẳng (P) nên R = d I ; P = x 1 + 2 y 1 - 2 z 1 + 2 1 2 + 2 2 + - 2 2 = 3 .