Trong không gian Oxyz, cho vecto a ⇀ ( - 3 ; 2 ; 1 ) và điểm A(4;6;-3). Tìm tọa độ điểm B thỏa mãn A B ⇀ = a ⇀
A. (7;4;-4)
B. (1;8;-2)
C. (-7;-4;4)
D. (-1;-8;2).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta biết rằng a → và b → cùng phương khi và chỉ khi a → = k b → với k là một số thực. Theo giả thiết ta có: b → = ( x 0 ; y 0 ; z 0 ) với x 0 = 2. Ta suy ra k = 1/2 nghĩa là l = x 0 /2
Do đó: −3 = y 0 /2 nên y 0 = -6
4 = z 0 /2 nên z 0 = 8
Vậy ta có b → = (2; −6; 8)

Theo giả thiết ta có c → = −2 a →
Do đó tọa độ của c → là: c → = (-2; 6; -8).

\(cos\left(\overrightarrow{b};\overrightarrow{a}-\overrightarrow{b}\right)=\dfrac{\overrightarrow{b}\left(\overrightarrow{a}-\overrightarrow{b}\right)}{\left|\overrightarrow{b}\right|.\left|\overrightarrow{a}-\overrightarrow{b}\right|}=\dfrac{\overrightarrow{a}.\overrightarrow{b}-\overrightarrow{b}^2}{1.\sqrt{3}}=\dfrac{2.1.cos\dfrac{\pi}{3}-1^2}{\sqrt{3}}=0\)
\(\Rightarrow\left(\overrightarrow{b};\overrightarrow{a}-\overrightarrow{b}\right)=90^0\)

Đáp án A.
Phương pháp
Cho hai điểm A x 1 ; y 1 ; z 1 ; B x 2 ; y 2 ; z 2 thì
A B → = x 2 − x 1 ; y 2 − y 1 ; z 2 − z 1
Cách giải
Áp dụng công thức ta có:
A B → = 1 − − 1 ; − 1 − 0 ; 2 − 1 = 2 ; − 1 ; 1
Gọi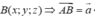
Chọn đáp án B.