Trong mặt phẳng với hệ tọa độ Oxy cho hình vuông ABCD. Điểm N(1;-2) thỏa mãn 2vecto NB+vecto NC=0 và điểm M(3;6) thuộc đường thẳng chứa cạnh AD. gọi H là hình chiếu vuong góc của A xuống đường thẳng DN. Xác định tọa độ các đỉnh của hình vuông ABCD biết khoảng cách từ H đến cạnh CD bằng \(\frac{12\sqrt{2}}{13}\) và đỉnh A có hoành độ là số nguyên lớn hơn 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
25 tháng 3 2021
Phương trình đường thẳng AM: \(ax+by-\dfrac{11}{2}a-\dfrac{1}{2}b=0\left(a^2+b^2\ne0\right)\)
Giả sử cạnh hình vuông có độ dài là \(a\)
\(AM^2=\dfrac{5}{4}a^2;AN^2=\dfrac{10}{9}a^2;MN^2=\dfrac{25}{36}a^2\)
Theo định lí cos: \(cosMAN=\dfrac{AM^2+AN^2-MN^2}{2.AM.AN}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\dfrac{\left|2a-b\right|}{\sqrt{5\left(a^2+b^2\right)}}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left(a-3b\right)\left(3a+b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=3b\\3a=-b\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AM:3x+y-17=0\\AM:x-3y-4=0\end{matrix}\right.\)
TH1: \(AM:3x+y-17=0\Rightarrow A:\left\{{}\begin{matrix}3x+y-17=0\\2x-y-3=0\end{matrix}\right.\Rightarrow A=\left(4;5\right)\)
TH2: \(AM:x-3y-4=0\Rightarrow A:\left\{{}\begin{matrix}x-3y-4=0\\2x-y-3=0\end{matrix}\right.\Rightarrow A=\left(1;-1\right)\)
CM
21 tháng 3 2017
Đáp án A.
Tọa độ điểm M 2 ; − 1 ; 1 trên mặt phẳng (Oxy) là M ' 2 ; − 1 ; 0 .
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2021
\(\overrightarrow{AB}=\left(-4;4\right)=-4\left(1;-1\right)\)
\(\Rightarrow\) Phương trình CD song song AB đi qua D có dạng:
\(1\left(x+6\right)+1\left(y+8\right)=0\Leftrightarrow x+y+14=0\)
Gọi M là trung điểm AB \(\Rightarrow M\left(-6;4\right)\)
Phương trình đường thẳng d qua M và vuông góc AB có dạng:
\(1\left(x+6\right)-1\left(y-4\right)=0\Leftrightarrow x-y+10=0\)
Gọi N là giao điểm CD và d \(\Rightarrow\) N là trung điểm CD do ABCD là hình thang cân
Tọa độ N là nghiệm: \(\left\{{}\begin{matrix}x+y+14=0\\x-y+10=0\end{matrix}\right.\) \(\Rightarrow N\left(-12;-2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_C=2x_N-x_D=...\\y_C=2y_N-y_D=...\end{matrix}\right.\)
CM
23 tháng 8 2018
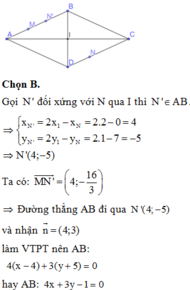
Gọi C= (x, y). Ta có A B → = 2 ; 1 B C → = x − 3 ; y .
Vì ABCD là hình vuông nên ta có A B → ⊥ B C → A B = B C
⇔ 2 x − 3 + 1. y = 0 x − 3 2 + y 2 = 5 ⇔ y = 2 3 − x 5 x − 3 2 = 5 ⇔ y = 2 3 − x x − 3 2 = 1 ⇔ x = 4 y = − 2 hoặc x = 2 y = 2 .
Với C 1 4 ; − 2 ta tính được đỉnh D 1 2 ; − 3 : thỏa mãn.
Với C 2 2 ; 2 ta tính được đỉnh D 2 0 ; 1 : không thỏa mãn.
Chọn B.
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2021
AB đi qua E và vuông góc BC nên nhận (1;-1) là 1 vtpt
Phương trình AB:
\(1\left(x+1\right)-1\left(y-1\right)=0\Leftrightarrow x-y+2=0\)
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x-y+2=0\\x+y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(-3;-1\right)\)
Đường thẳng d qua M và song song AB có pt:
\(1\left(x+1\right)-1\left(y+1\right)=0\Leftrightarrow x-y=0\)
Gọi N là giao điểm d và BC \(\Rightarrow N\) là trung điểm BC
Tọa độ N là nghiệm: \(\left\{{}\begin{matrix}x-y=0\\x+y-4=0\end{matrix}\right.\) \(\Rightarrow N\left(2;2\right)\Rightarrow C\left(7;5\right)\)
Đường thẳng AD qua M và song song BC có pt:
\(1\left(x+1\right)+1\left(y+1\right)=0\Leftrightarrow x+y+2=0\)
A là giao điểm AB và AD nên tọa độ là nghiệm: \(\left\{{}\begin{matrix}x-y+2=0\\x+y+2=0\end{matrix}\right.\) \(\Rightarrow A\left(-2;0\right)\)
\(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow\) tọa độ D