Trong không gian với hệ tọa độ Oxyz cho điểm A (3;2;-1) và đường thẳng d : x = t y = t z = 1 + t
Viết phương trình mặt phẳng (P) chứa d sao cho khoảng cách từ A đến (P) là lớn nhất.
A. 2x + y - 3z + 3 = 0
B. x + 2y - z - 1 = 0
C. 3x + 2y - z + 1 = 0
D. 2x - y - 3z + 3 = 0

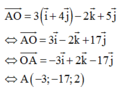

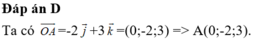
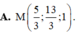
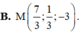
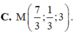
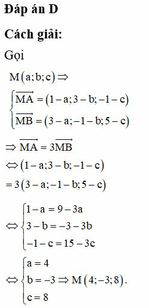
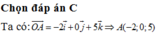
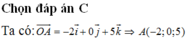
Chọn A
+ d qua M0 (0;0;1) có vectơ chỉ phương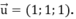
+ Gọi H, K lần lượt là hình chiếu của A lên (P) và d. Ta có: d(A, (P)) = AH ≤ AK
Đẳng thức xảy ra khi và chỉ khi H ≡ K. Do đó d(A, (P))max = AK
Khi đó (P) đi M0 (0;0;1) nhận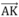 làm vectơ pháp tuyến.
làm vectơ pháp tuyến.