Trong không gian cho hai điểm A(x; y; z), B(m, n, p) thay đổi nhưng luôn thỏa mãn các điều kiện x 2 + y 2 + z 2 = 4, m 2 + n 2 + p 2 = 9. Vectơ AB → có độ dài nhỏ nhất là:
A. 5
B. 1
C. 13
D. Không tồn tại
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điểm cần tìm M(x;y;z) ta có điều kiện cách đều hai mặt phẳng là
![]()
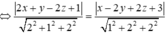
![]()
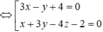
Vậy tập hợp các điểm này nằm trên hai mặt phẳng vuông góc với nhau (hai mặt phẳng này được gọi là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng).
Chọn đáp án C.
Chọn đáp án C.

Phương trình mặt phẳng trung trực của AB là ![]()
Đường thẳng cần tìm d cách đều hai điểm A, B nên sẽ thuộc mặt phẳng α
Lại có ![]() hay
hay 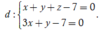
Chọn x = t ta được: 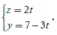
Chọn C.

Đáp án B
Phương pháp:
-Sử dụng kiến thức về vị trí của một điểm đối với mặt phẳng.
Cho mặt phẳng P : A x + B y + C z + D = 0 và hai điểm

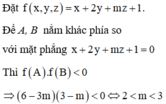

Đáp án B.
Phương pháp:
-Sử dụng kiến thức về vị trí của một điểm đối với mặt phẳng.
Cho mặt phẳng ![]()
và hai điểm ![]()
Đặt:
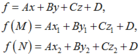
Hai điểm M, N nằm khác phía so với mặt phẳng (P)
![]()
Cách làm:
Đặt ![]()
Để A, B nằm khác phía so với mặt phẳng
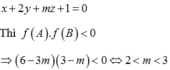

Đáp án D
Ta có: A B → = ( - 3 ; - 2 ; 2 ) ; n ( P ) → = ( 1 ; - 3 ; 2 )
Khi đó: A B → ; n ( P ) → = 0 ; 8 ; 12 ⇒ n ( Q ) → = ( 0 ; 2 ; 3 )
Suy ra (Q): 2y + 3z – 11 = 0
Đáp án B
Từ giả thiết suy ra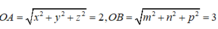
Do đó AB ≥ |OA - OB| = 1. Dấu bằng xảy ra khi O nằm ngoài đoạn AB. Suy ra đáp án đúng là B.
Hai đáp án A, D sai do nhầm OA = x 2 + y 2 + z 2 = 4; OB = m 2 + n 2 + p 2 = 9
Đáp án C sai do nhầm với câu hỏi vectơ AB→ có độ dài lớn nhất