Cho 2 điểm phân biệt A ( xA ; yA ) và ( xB ; yB ). Ta nói điểm M chia đoạn thẳng AB theo tỉ số k nếu \(\overrightarrow{MA}=k\overrightarrow{MB}\left(k\ne1\right)\). Chứng minh rằng:
\(\hept{\begin{cases}x_M=\frac{x_A-kx_B}{1-k}\\y_M=\frac{y_A-ky_B}{1-k}\end{cases}}\)


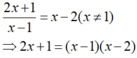

Giả sử M(x;y;z)M(x;y;z) thỏa mãn −−→MA=k−−→MBMA→=kMB→ với k≠1k≠1.
Ta có −−→MA=(x1–x;y1–y;z1–z),−−→MB=(x2–x;y2–y;z2–z)MA→=(x1–x;y1–y;z1–z),MB→=(x2–x;y2–y;z2–z)
−−→MA=k−−→MB⇔⎧⎪⎨⎪⎩x1–x=k(x2–x)y1–y=k(y2–y)z1–z=k(z2–z)⇔⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩x=x1–kx21–ky=y1–ky21–kz=z1–kz21–kMA→=kMB→⇔{x1–x=k(x2–x)y1–y=k(y2–y)z1–z=k(z2–z)⇔{x=x1–kx21–ky=y1–ky21–kz=z1–kz21–k
mấy bạn ơi hộ mình đi !!!