Tính diện tích hình phẳng giới hạn bởi các đường:
y = ln x ; x = 1 e ; x = e và trục hoành.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(V=\pi \int ^4_1[x^{\frac{1}{2}}e^{\frac{x}{2}}]^2dx=\pi \int ^4_1(xe^x)dx\)
\(=\pi \int ^4_1xd(e^x)=\pi (|^4_1xe^x-\int ^4_1e^xdx)\)
\(=\pi |^4_1(xe^x-e^x)=\pi (3e^4)=3\pi e^4\)
2.
\(V=\pi \int ^1_0(x\sqrt{\ln (x^3+1)})^2dx=\pi \int ^1_0x^2\ln (x^3+1)dx\)
\(=\frac{1}{3}\pi \int ^1_0\ln (x^3+1)d(x^3+1)\)
\(=\frac{1}{3}\pi \int ^2_1ln tdt=\frac{1}{3}\pi (|^2_1t\ln t-\int ^2_1td(\ln t))\)
\(=\frac{1}{3}\pi (|^2_1t\ln t-\int ^2_1dt)=\frac{1}{3}\pi |^2_1(t\ln t-t)=\frac{1}{3}\pi (2\ln 2-1)\)

Đồ thị hàm số y = x3 - x; y = x - x2 .Đặt f1(x) = x3 - x, f2(x) = x - x2
Ta có f1(x) - f2(x) = 0 <=> x3 + x2 - 2x = 0 có 3 nghiệm x = -2; x = 0 ; x = 1
Vậy : Diện tích hình phẳng đã cho là :
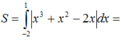
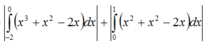
= 37 12

Chọn C.
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:
(x – 1) ln(x + 1) = 0 <=> x = 1 hoặc x = 0
→ Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = (x – 1) ln(x = 1) và trục hoành là
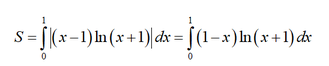
Đặt u = ln ( x + 1 ) d v = ( 1 - x ) d x ⇒ d u = 1 x + 1 d x v = 2 x - x 2 2
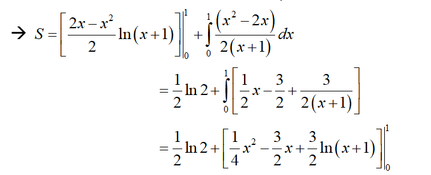
= 1 2 ln 2 - 5 4 + 3 2 ln 2 = - 5 4 + 2 ln 2

Đáp án B
Điều kiện: x > 0
Phương trình hoành độ giao điểm của đồ thị hàm số y=x.lnx và trục hoành là
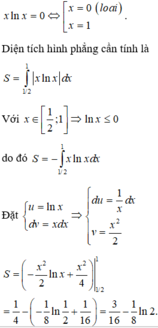

Đáp án B
Điều kiện: x > 0
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là
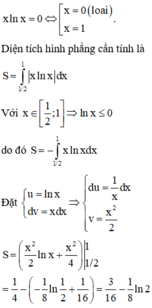
Diện tích cần tính là: