Cho tam giác ABC. Trên tia BC lấy BA' =2BC, trên tia CA lấy CB' =2CA; trên tia AB lấy AC' = 2AB. Chứng minh hai tam giác ABC và A'B'C' có cùng trọng tâm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


nhờ bạn nào đó vẽ hình cho nha, tui ko bt vẽ.![]()
giải
tam giác ABC cân tại A \(\Rightarrow\) góc ABC = góc ACB = \(\dfrac{180^o-50^o}{2}=75^o\)
❆góc ABC = \(75^o\) \(\Rightarrow\) góc DBA = \(180^o-75^o=105^o\)
\(\Delta DAB\) có DB=BA \(\Rightarrow\) \(\Delta\) DBA cân tại B
\(\Rightarrow\) góc DAB = góc ADB = \(\dfrac{180^o-105^o}{2}=32,5^o\)
❆ góc ACB = \(75^o\) \(\Rightarrow\) góc ACE = \(180^o-75^o=105^o\)
\(\Delta ACE\) có AC=CE \(\Rightarrow\) tam giác ACE cân tại C
\(\Rightarrow\) góc CAE = góc CEA = \(\dfrac{180^o-105^o}{2}=32,5^o\)
❆ ta có : góc DAE = góc DAB + góc CAE + góc BAC
= \(32,5^o+32,5^o+50^o=125^o\)
vậy góc DAE = \(125^o\)

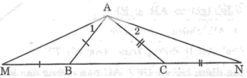
Trong ΔABC, ta có AC > AB
Suy ra: ∠(ABC) > ∠(ACB) (đối diện với cạnh lớn hơn là góc lớn hơn) (1)
Ta có: AB = BM (gt) ⇒ ΔABM cân tại B
Suy ra: ∠(AMB) = ∠A1(tính chất tam giác cân)
Trong ΔABM, ta có ∠(ABC) là góc ngoài tại đỉnh B
Suy ra: ∠(ABC) = ∠(AMB) + ∠A1 hay : ∠(ABC) = 2.∠(AMB)
Suy ra: ∠(AMB) = 1/2 ∠(ABC) (2)
Lại có: AC = CN (gt) ⇒ ΔACN cân tại C
Suy ra: ∠(ANC) = ∠A2(tính chất tam giác cân)
Trong ΔACN, ta có ∠(ACB) là góc ngoài tại đỉnh C
Suy ra: ∠(ACB) = ∠(ANC) + ∠A2 hay ∠(ACB) = 2∠(ANC)
Suy ra: ∠(ANC) = 1/2 ∠(ACB) (3)
Từ (1), (2) và (3) suy ra: ∠(AMB) > ∠(ANC) .