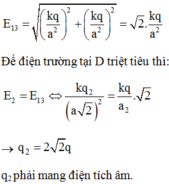Cho q1=....C; m=...gam; treo trên 1 sợi dây mảnh đặt trong không khí .Đưa q2 lại gần q1 .Tìm dấu và độ lớn của q2 để lực căng dây giảm một nửa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án: A
Vì cường độ điện trường tại M bằng 0 nên hai vecto E 1 do q1 gây ra và E 2 do q2 gây ra phải ngược chiều và cùng độ lớn nên M nằm trên đường thẳng AB
r1 < r2 và r1 + AB = r2 nên q1 và q2 trái dấu và |q1| < |q2|
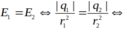
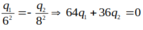
và q1 + q2 = 7.10-8
=> q1= -9.10-8 C, q2= 16.10-8 C

a. Xác định lực khi cho q1, q2 tác dụng lên q3
Hợp lực tác dụng lên q3:
\(\vec{F_3}=\vec{F_{13}}+\vec{F_{23}}\)
Suy ra độ lớn:
\(F_3=F_{23}-F_{13}\) (1)
\(F_{13}=9.10^9.\dfrac{|q_1.q_3|}{AC^2}=9.10^9.\dfrac{|6.10^{-9}.2.10^{-9}|}{0,06^2}=3.10^{-5}N\)
\(F_{23}=9.10^9.\dfrac{|q_2.q_3|}{BC^2}=9.10^9.\dfrac{|3.10^{-9}.2.10^{-9}|}{0,03^2}=6.10^{-5}N\)
Thay vào (1) ta tìm được \(F_3=3.10^{-5}(N)\)
b. Ý này tương tự bạn nhé, phân tích lực --> Tổng hợp lực --> Rút ra biểu thức độ lớn --> Thay số.