Mọi người giúp mình bài này với ạBài 1: Một vật có khối lượng m=1kg trượt không vận tốc ban đầu từ đỉnh B xuống chân dốc C. Cho dốc nghiêng BC cao 10m dài 20m; lấy g=10m/s2. Hệ số ma sát giữa vật và mặt phẳng ngiêng là u=0,1a: Tính vận tốc của vật ở chân dốc Cb: Đến mặt phẳng ngang vật va chạm mềm với vật M=1,5kg đang nằm yên, coi độ lớn vận tốc của vật không thay đổi khi chuyển từ mặt...
Đọc tiếp
Mọi người giúp mình bài này với ạ
Bài 1: Một vật có khối lượng m=1kg trượt không vận tốc ban đầu từ đỉnh B xuống chân dốc C. Cho dốc nghiêng BC cao 10m dài 20m; lấy g=10m/s2. Hệ số ma sát giữa vật và mặt phẳng ngiêng là u=0,1
a: Tính vận tốc của vật ở chân dốc C
b: Đến mặt phẳng ngang vật va chạm mềm với vật M=1,5kg đang nằm yên, coi độ lớn vận tốc của vật không thay đổi khi chuyển từ mặt phẳng nghiêng sang mặt phẳng ngang. Sau va chạm hai vật dính vào nhau và chuyển động với cùng vận tốc \(\overrightarrow{v}\). Tính độ lớn của v
Chú ý: Bài toán phải được giải bằng cách áp dụng các định luật bảo toàn, không dùng phương pháp động lực học
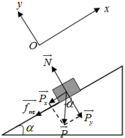
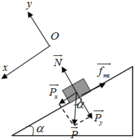
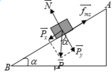
a)Xét tam giác vuông: \(cos\alpha=\dfrac{\sqrt{20^2-10^2}}{20}=\sqrt{3}\)
Độ biến thiên động năng:
\(\Delta A=W_{đC}-W_{đB}=\dfrac{1}{2}m\left(v_C^2-v_B^2\right)=\dfrac{1}{2}mv_C^2\)
Mà \(\Delta A=A_{ms}+A_N+A_P=F_{ms}\cdot s+A_P=-\mu mgscos\alpha+mgh\)
\(\Rightarrow\dfrac{1}{2}mv_C^2=-\mu mgscos\alpha+mgh\Rightarrow\dfrac{1}{2}\cdot1\cdot v_C^2=-0,1\cdot1\cdot10\cdot\sqrt{3}+1\cdot10\cdot10\)
\(\Rightarrow v_C=14,02\)m/s
b)Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
\(\Rightarrow m_1v_1+m_2v_2=\left(m_1+m_2\right)v\Rightarrow1\cdot0+1,5\cdot14,02=\left(1+1,5\right)v\)
\(\Rightarrow v=8,412\)m/s