cho tam giác ABC nhọn AB=AC, nội tiếp ( O ) gọi D là điểm thuộc cung BC không chứa A, B là giao điểm của BC và AD
chứng minh l; góc AEB= góc ABD
AC^2=AD.AE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Ta có: ^ACD = ^ACB + ^BCD; ^AEC = ^ABC + ^BAD
Mà ^ACB = ^ABC (∆ABC cân tại A); ^BCD = ^BAD (hai góc nội tiếp cùng chắn một cung)
nên ^ACD = ^AEC (1)
+) Dễ có: ∆AEB ~ ∆CED (g.g) nên \(\frac{AB}{CD}=\frac{AE}{CE}=\frac{AC}{CD}\)(2)
Từ (1) và (2), ta có: ^ACD = ^AEC và \(\frac{AE}{CE}=\frac{AC}{CD}\)nên ∆AEC ~ ACD (c.g.c)
\(\Rightarrow\frac{AC}{AD}=\frac{AE}{AC}\Rightarrow AC^2=AE.AD\)(đpcm)
vì AB =AC => sđ cung AB = sđ cung AC
=> 1/2 ( sđ CD + sđ AB ) =1/2 ( sđ CD + sđ AC )
=> AEB = 1/2 sđ AD =ABD
CM tam giác ABD ~ tam giác AEB ( g-g) => AC^2 = AD.AE

a)Xét (O) có:
góc PDA và góc PIA là 2 góc có đỉnh nằm trong đường tròn
=>góc PDA=\(\dfrac{sđ\stackrel\frown{AP}+sđ\stackrel\frown{BM}}{2}\),góc PIA=\(\dfrac{sđ\stackrel\frown{AP}+sđ\stackrel\frown{MC}}{2}\)
mà \(\stackrel\frown{BM}=\stackrel\frown{MC}\)(M là điểm chính giữa)
=> góc PDA = góc PIA
Xét tứ giác AIDP có
2 đỉnh D và I kề nhau cùng nhìn cạnh AP
góc PDA = góc PIA (cmt)
=>AIDP là tứ giác nội tiếp (dhnb)
b)Xét (O) có
PAB và PCB là 2 góc nội tiếp cùng chắn cung BP
=> góc PAB = góc PCB
mà góc PAB = góc PID ( tứ giác AIDP nội tiếp)
=> góc PCB= góc PID
=>ID//BC
c)CMTT câu trên ta được IE//BC
Mà ID//BC
=>IE trùng với ID(tiên đề ơ clit)
=> 3 ddierm D,I,E thẳng hàng

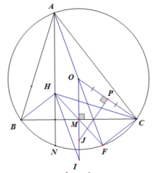
Ta có NHC = ABC (cùng phụ với HCB) (1)
Vì ABDC là tứ giác nội tiếp nên ABC = ADC (2)
Vì D và E đối xứng nhau qua AC nên AC là trung trực DE suy ra
∆ADC = ∆AEC (c.c.c) => ADC = AEC (3)
Tương tự ta có AEK = ADK
Từ (1), (2), (3) suy ra NHC = AEC => AEC + AHC = NHC + AHC = 180o
Suy ra AHCE là tứ giác nội tiếp => ACH = AEK = ADK (đpcm)
giúp mình với
Bạn xem lại đề, AD đâu có bằng AB đâu mà góc AEB= góc ABD