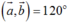Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Câu 4:
Áp dụng định lý Pytago
\(BC^2=AB^2+AC^2\Rightarrow BC=2\)
Ta có:
\(\overrightarrow{CA}.\overrightarrow{BC}=-\overrightarrow{CA}.\overrightarrow{CB}=-\dfrac{CA^2+CB^2-AB^2}{2}=-\dfrac{2+4-2}{2}=-2\)
Câu 5:
Gọi M là trung điểm BC
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Mà: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Câu 6:
\(\left|\overrightarrow{a}-\overrightarrow{b}\right|=3\)
\(a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=9\)
\(\overrightarrow{a}.\overrightarrow{b}=\dfrac{1^2+2^2-9}{2}=-2\)
Câu 7:
\(\left|\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{CD}\right|=\left|\overrightarrow{DB}+\overrightarrow{CD}\right|\)
\(=\left|\overrightarrow{DB}-\overrightarrow{DC}\right|=\left|\overrightarrow{CB}\right|=BC=a\)
a → = 1 2 + 3 2 = 2 , b → = − 2 3 2 + 6 2 = 48 = 4 3
a → . b → = 1. − 2 3 + 3 .6 = 4 3
cos a → , b → = a → . b → a → b → = 4 3 2.4 3 = 1 2 ⇒ a → , b → = 60
Chọn D
Áp dụng hệ quả của định lí cosin ta có
chào tôi tên trợ học lớp 7
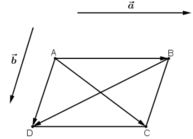
Có hai vec tơ a→, b→ bất kì như hình vẽ.
Vẽ hình bình hành ABCD sao cho 
Ta có:
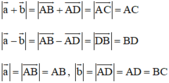
Do đó
a)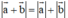 
⇔ AC = AB + BC ⇔ B nằm giữa A và C
⇔ 
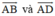cùng hướng hay a→ và b→ cùng hướng.
b)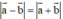 
⇔ AC = BD
⇔ ABCD là hình chữ nhật
⇔ AB ⊥ CD hay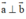 
a) \(\overrightarrow {MN} = 3\overrightarrow a \)có độ dài bằng 3 lần vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \)
Suy ra, từ điểm M vẽ vectơ MN với độ dài là 6 ô vuông và có hướng từ trái sang phải
\(\overrightarrow {MP} = - 3\overrightarrow b \)có độ dài bằng 3 lần vectơ \( - \overrightarrow b \), ngược hướng với vectơ \(\overrightarrow b \)
Suy ra, từ điểm M vẽ vectơ MP với độ dài là 3 đường chéo ô vuông và có hướng từ trên xuống dưới chếch sang trái
b) Hình vuông với cạnh bằng 1 thì ta tính được đường chéo có độ dài là \(\sqrt 2 \); \(\left| {\overrightarrow b } \right| = \sqrt 2 \) . Suy ra:
\(\left| {3\overrightarrow b } \right| = 3\left| {\overrightarrow b } \right| = 3\sqrt 2 \); \(\left| { - 3\overrightarrow b } \right| = 3\left| {\overrightarrow { - b} } \right| = 3\sqrt 2 \); \(\left| {2\overrightarrow a + 2\overrightarrow b } \right| = \left| {2\left( {\overrightarrow a + \overrightarrow b } \right)} \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right|\)
Từ điểm cuối của vectơ \(\overrightarrow a \) vẽ một vectơ bằng vectơ \(\overrightarrow b \) ta có \(\overrightarrow c = \overrightarrow a + \overrightarrow b \)
Áp dụng định lý cosin ta tính được độ dài của vectơ \(\overrightarrow c \)là \(\left| {\overrightarrow c } \right| = \sqrt {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - 2\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \left( {\widehat {\overrightarrow a ,\overrightarrow b }} \right)} = \sqrt {{2^2} + {{\sqrt 2 }^2} - 2.2.\sqrt 2 .\cos \left( {135^\circ } \right)} = \sqrt {10} \)
\( \Rightarrow \left| {2\overrightarrow a + 2\overrightarrow b } \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right| = 2\left| {\overrightarrow c } \right| = 2\sqrt {10} \)
Lời giải:
Nếu bạn có $\overrightarrow{a}(x_1,y_1);\overrightarrow{b}(x_2,y_2)$ thì:
$\overrightarrow{a}.\overrightarrow{b}=x_1x_2+y_1y_2$
Áp dụng vào bài toán:
$\overrightarrow{a}.\overrightarrow{b}=1(-2)+3.1=-2+3=1$
cos a → , b → = − 3.2 + 3 3 .2 3 − 3 2 + 3 3 2 . 2 2 + 2 3 2 = 12 6.4 = 1 2
Do đó, góc giữa hai vecto là: a → , b → = 60 °
ĐÁP ÁN D
Ta có: 1 2 a → − b → = − − 1 2 a → + b →
Do đó, hai vecto 1 2 a → − b → ; − 1 2 a → + b → cùng phương
Đáp án C
Chọn A.
Ta có:
nên