Cho hàm số \(y=f\left(x\right)\) liên tục trên đoạn [a; b]. Nếu \(f\left(a\right).f\left(b\right)>0\) thì phương trình \(f\left(x\right)=0\) có nghiệm hay không trong khoảng (a;b) ? Cho ví dụ minh họa ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2022
\(f\left(x\right)-\left(x+1\right)f'\left(x\right)=2x.f^2\left(x\right)\)
\(\Rightarrow\dfrac{f\left(x\right)-\left(x+1\right)f'\left(x\right)}{f^2\left(x\right)}=2x\)
\(\Rightarrow\left[\dfrac{x+1}{f\left(x\right)}\right]'=2x\)
Lấy nguyên hàm 2 vế:
\(\dfrac{x+1}{f\left(x\right)}=\int2xdx=x^2+C\)
Thay \(x=1\Rightarrow\dfrac{2}{f\left(1\right)}=1+C\Rightarrow C=0\)
\(\Rightarrow f\left(x\right)=\dfrac{x+1}{x^2}\Rightarrow\int\limits^2_1\left(\dfrac{1}{x}+\dfrac{1}{x^2}\right)dx=\left(lnx-\dfrac{1}{x}\right)|^2_1=ln2+\dfrac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 4 2021
Đặt \(g\left(x\right)=f\left(x+\dfrac{1}{3}\right)-f\left(x\right)\)
Hiển nhiên \(g\left(x\right)\) cũng liên tục trên R
Ta có: \(g\left(0\right)=f\left(\dfrac{1}{3}\right)-f\left(0\right)\)
\(g\left(\dfrac{2}{3}\right)=f\left(1\right)-f\left(\dfrac{2}{3}\right)\)
\(g\left(\dfrac{1}{3}\right)=f\left(\dfrac{2}{3}\right)-f\left(\dfrac{1}{3}\right)\)
Cộng vế với vế:
\(g\left(0\right)+g\left(\dfrac{1}{3}\right)+g\left(\dfrac{2}{3}\right)=f\left(1\right)-f\left(0\right)=0\)
- Nếu tồn tại 1 trong 3 giá trị \(g\left(0\right);g\left(\dfrac{1}{3}\right);g\left(\dfrac{2}{3}\right)\) bằng 0 thì hiển nhiên pt có nghiệm
- Nếu cả 3 giá trị đều khác 0 \(\Rightarrow\) tồn tại ít nhất 2 trong 3 giá trị \(g\left(0\right)\) ; \(g\left(\dfrac{1}{3}\right)\) ; \(g\left(\dfrac{2}{3}\right)\) trái dấu
\(\Rightarrow\) Luôn tồn tại ít nhất 1 trong 3 tích số: \(g\left(0\right).g\left(\dfrac{1}{3}\right)\) ; \(g\left(0\right).g\left(\dfrac{2}{3}\right)\) ; \(g\left(\dfrac{1}{3}\right).g\left(\dfrac{2}{3}\right)\) âm
\(\Rightarrow\) Pt \(g\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left[0;1\right]\)
HT
21 tháng 3 2021
Đang học Lý mà thấy bài nguyên hàm hay hay nên nhảy vô luôn :b
\(I_1=\int\limits^1_0xf\left(x\right)dx\)
\(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=xdx\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=\dfrac{1}{2}x^2\end{matrix}\right.\)
\(\Rightarrow\int xf\left(x\right)dx=\dfrac{1}{2}x^2f\left(x\right)-\dfrac{1}{2}\int x^2f'\left(x\right)dx\)
\(\Rightarrow\int\limits^1_0xf\left(x\right)dx=\dfrac{1}{2}x^2|^1_0-\dfrac{1}{2}\int\limits^1_0x^2f'\left(x\right)dx=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{1}{2}\int\limits^1_0\left[f'\left(x\right)\right]^2dx=\dfrac{3}{10}\Rightarrow\int\limits^1_0x^2f'\left(x\right)dx=\dfrac{3}{5}\)
Đoạn này hơi rối xíu, ông để ý kỹ nhé, nhận thấy ta có 2 dữ kiện đã biết, là: \(\int\limits^1_0\left[f'\left(x\right)\right]^2dx=\dfrac{9}{5}and\int\limits^1_0x^2f'\left(x\right)dx=\dfrac{3}{5}\) có gì đó liên quan đến hằng đẳng thức, nên ta sẽ sử dụng luôn
\(\int\limits^1_0\left[f'\left(x\right)+tx^2\right]^2dx=0\)
\(\Leftrightarrow\int\limits^1_0\left[f'\left(x\right)\right]^2dx+2t\int\limits^1_0x^2f'\left(x\right)dx+t^2\int\limits^1_0x^4dx=0\)
\(\Leftrightarrow\dfrac{9}{5}+\dfrac{6}{5}t+\dfrac{1}{5}t^2=0\) \(\left(\int\limits^1_0x^4dx=\dfrac{1}{5}x^5|^1_0=\dfrac{1}{5}\right)\)\(\)\(\Leftrightarrow t=-3\Rightarrow\int\limits^1_0\left[f'\left(x\right)-3x^2\right]^2dx=0\)
\(\Leftrightarrow f'\left(x\right)=3x^2\Leftrightarrow f\left(x\right)=x^3+C\)
\(\Rightarrow\int\limits^1_0f\left(x\right)dx=\int\limits^1_0x^3dx=\dfrac{1}{4}x^4|^1_0=\dfrac{1}{4}\)
P/s: Có gì ko hiểu hỏi mình nhé !
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Theo em ý kiến của bạn Nam là đúng.
Ta có: Hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0}\) nên \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Hàm số \(y = g\left( x \right)\) không liên tục tại \({x_0}\) nên \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) \ne g\left( {{x_0}} \right)\)
Do đó \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) + \mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) \ne f\left( {{x_0}} \right) + g\left( {{x_0}} \right)\)
Vì vậy hàm số không liên tục tại x0.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2022
\(\int\limits^3_{-1}f\left(\left|x\right|\right)dx=\int\limits^0_{-1}f\left(\left|x\right|\right)dx+\int\limits^1_0f\left(\left|x\right|\right)dx+\int\limits^3_1f\left(\left|x\right|\right)dx\)
\(=\int\limits^0_{-1}f\left(-x\right)dx+\int\limits^1_0f\left(x\right)dx+\int\limits^3_1f\left(x\right)dx\)
\(=\int\limits^1_0f\left(x\right)dx+\int\limits^1_0f\left(x\right)dx+\int\limits^3_1f\left(x\right)dx\)
\(=3+3+6=12\)
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\), \(f\left( x \right) = \frac{{{x^2} - 2x}}{x}\) là hàm phân thức hữu tỉ nên liên tục trên từng khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Ta có: \(f\left( 0 \right) = a\)
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \frac{{{x^2} - 2x}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{x\left( {x - 2} \right)}}{x} = \mathop {\lim }\limits_{x \to 0} \left( {x - 2} \right) = 0 - 2 = - 2\)
Để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thì hàm số \(y = f\left( x \right)\) phải liên tục tại điểm \({x_0} = 0\). Khi đó:
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right) \Leftrightarrow a = - 2\).
Vậy với \(a = - 2\) thì hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\), \(f\left( x \right) = \frac{{{x^2} - 4}}{{x + 2}}\) là hàm phân thức hữu tỉ nên liên tục trên từng khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
Ta có: \(f\left( { - 2} \right) = a\)
\(\mathop {\lim }\limits_{x \to - 2} f\left( x \right) = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} - 4}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \left( {x - 2} \right) = - 2 - 2 = - 4\)
Để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thì hàm số \(y = f\left( x \right)\) phải liên tục tại điểm \({x_0} = - 2\). Khi đó:
\(\mathop {\lim }\limits_{x \to - 2} f\left( x \right) = f\left( { - 2} \right) \Leftrightarrow a = - 4\).
Vậy với \(a = - 4\) thì hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Trên các khoảng \(\left( { - \infty ;5} \right)\) và \(\left( {5; + \infty } \right)\), \(f\left( x \right) = \frac{{{x^2} - 25}}{{x - 5}}\) là hàm phân thức hữu tỉ nên liên tục trên từng khoảng \(\left( { - \infty ;5} \right)\) và \(\left( {5; + \infty } \right)\).
Ta có: \(f\left( 5 \right) = a\)
\(\mathop {\lim }\limits_{x \to 5} f\left( x \right) = \mathop {\lim }\limits_{x \to 5} \frac{{{x^2} - 25}}{{x - 5}} = \mathop {\lim }\limits_{x \to 5} \frac{{\left( {x - 5} \right)\left( {x + 5} \right)}}{{x - 5}} = \mathop {\lim }\limits_{x \to 5} \left( {x + 5} \right) = 5 + 5 = 10\)
Để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thì hàm số \(y = f\left( x \right)\) phải liên tục tại điểm \({x_0} = 5\). Khi đó: \(\mathop {\lim }\limits_{x \to 5} f\left( x \right) = f\left( 5 \right) \Leftrightarrow a = 10\).
Vậy với \(a = 10\) thì hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
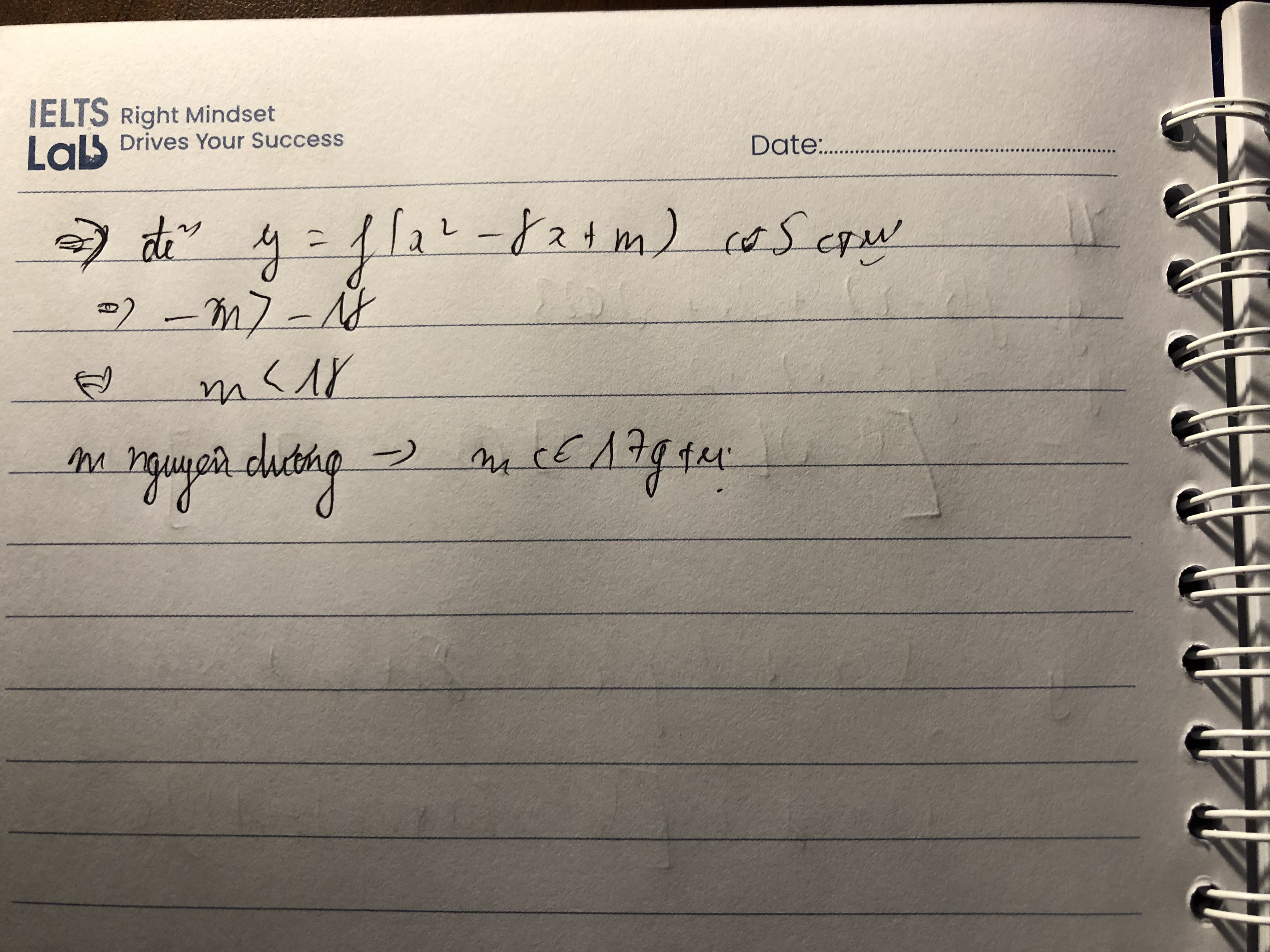
Tham khảo: