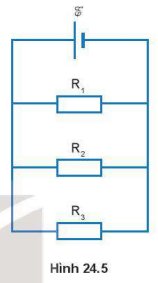
Cho mạch điện như Hình 24.5. Suất điện động E = 10 V, bỏ qua điện trở trong của nguồn. Các giá trị điện trở R1 = 20 Ω; R2 = 40 Ω, R3 = 50 Ω.
a) Tính cường độ dòng điện chạy qua điện trở R1.
b) Tính cường độ dòng điện I chạy qua mạch chính.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Mạch ngoài: \(\left(R_2//R_3\right)ntR_1\)
Điện trở mạch AB là:
\(R_{AB}=R_1+\dfrac{R_2R_3}{R_2+R_3}=3+\dfrac{4\cdot6}{4+6}=5,4\Omega\)
b) Cường độ dòng điện ở mạch chính:
\(I=\dfrac{E}{R_{AB}+r}=\dfrac{12}{5,4+0,6}=2A\)
Hiệu điện thế qua điện trở \(R_1\):
\(U_1=I_1R_1=2\cdot3=6V\)
Hiệu điện thế ở \(R_2,R_3\):
\(U_{23}=U-U_1=I\cdot R_{AB}-U_1=2\cdot5,4-6=4,8V\)
Cường độ dòng điện đi qua \(R_2,R_3\):
\(I_2=I_3=\dfrac{U_{23}}{R_{23}}=\dfrac{4,8}{\dfrac{R_2R_3}{R_2+R_3}}=\dfrac{4,8}{\dfrac{4\cdot6}{4+6}}=2A\)
Ta có: R1 ∥ R2 ∥ R3
Điện trở tương đương của mạch là: \(\frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}} \Rightarrow {R_{td}} = \frac{{200}}{{19}}\Omega \)
a) Cường độ dòng điện chạy qua điện trở R1: I1 = \(\frac{\xi }{{{R_1}}} = \frac{{10}}{{20}}\)= 0,5(A)
b) Cường độ dòng điện chạy qua mạch điện chính: I = \(\frac{\xi }{{{R_{td}}}} = \frac{{10}}{{\frac{{200}}{{19}}}}\)= 0,95(A).