Cho điểm A nằm ngoài (O; R), kẻ tiếp tuyến AB, AC của (O) (B, C là tiếp điểm). AO cắt BC tại H, kẻ cát tuyến ADE của (O) cắt đoạn BH, kẻ OI ⏊ DE tại I. a) Chứng minh ABIO nội tiếp và OH.OA = R2. b) Tiếp tuyến tại E của (O) cắt OI tại K. Chứng minh: D, K, E, O, H cùng thuộc một đường tròn. c) Chứng minh K, B, C thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

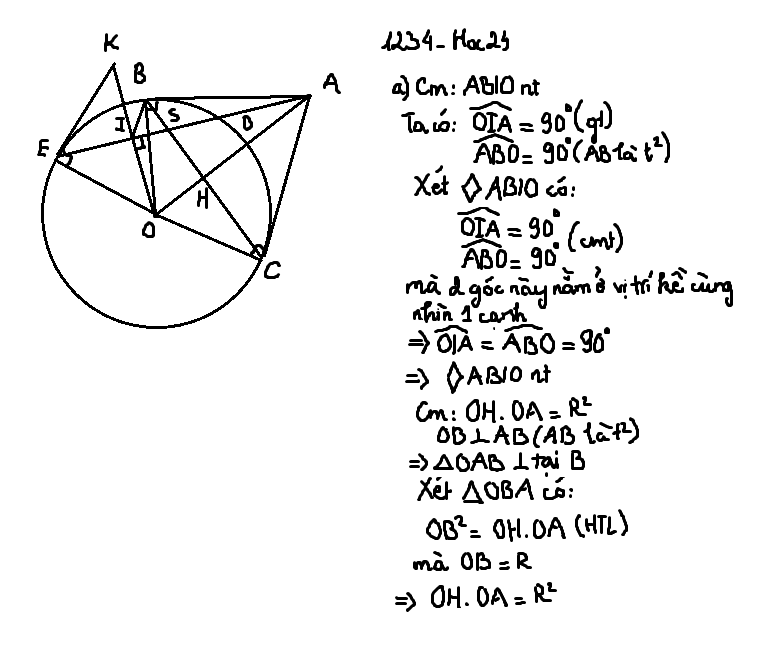

a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
c: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(1\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AD=AH\cdot AO\)
hay \(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
\(\widehat{HAE}\) chung
Do đó: ΔAEH\(\sim\)ΔAOD
Suy ra: \(\widehat{AHE}=\widehat{ADO}=\widehat{BDE}\)

Qua điểm thứ nhất: 0 tam giác
Qua điểm thứ 2: Thêm 1 tam giác
Qua điểm thứ 3: Thêm 2 tam giác
Qua điểm thứ 4: Thêm 3 tam giác
...
...
Qua điểm thứ 10: Thêm 9 tam giác
Tổng số tam giác là: 0+1+2+3+...+9 = 45 (tam giác)
Đáp số: 45 (tam giác)
Qua điểm thứ nhất: 0 tam giác
Qua điểm thứ 2: Thêm 1 tam giác
Qua điểm thứ 3: Thêm 2 tam giác
Qua điểm thứ 4: Thêm 3 tam giác
...
...
Qua điểm thứ 10: Thêm 9 tam giác
Tổng số tam giác là: 0+1+2+3+...+9 = 45 (tam giác)
Đáp số: 45 (tam giác)

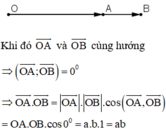
a) Ta có:

Ta thấy hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) cùng hướng nên \(\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = 0^\circ \)
\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = a.b.\cos 0^\circ = ab\)
b) Ta có:

Ta thấy hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) ngược hướng nên \(\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = 180^\circ \)
\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = a.b.\cos 180^\circ = - ab\)
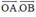 trong hai trường hợp:
trong hai trường hợp: