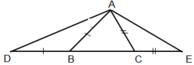
Cho tam giác ABC có AB=AC. Trên tia đối của tia BC và CB lấy theo thứ tự hai điểm D và E sao cho BD= CE; M là trung điểm của BC.
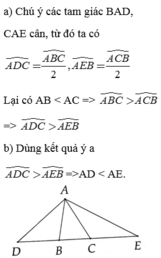
a) CMR: AD= AE
b) CMR: AM là tia phân giác của góc DAE
c) Từ B và C kẻ BH và CK theo thứ tự vuông góc với AD và AE. CMR: BH= CK ( H€ AD, K€ AE )
d) CMR: AM, BH, CK đồng quy

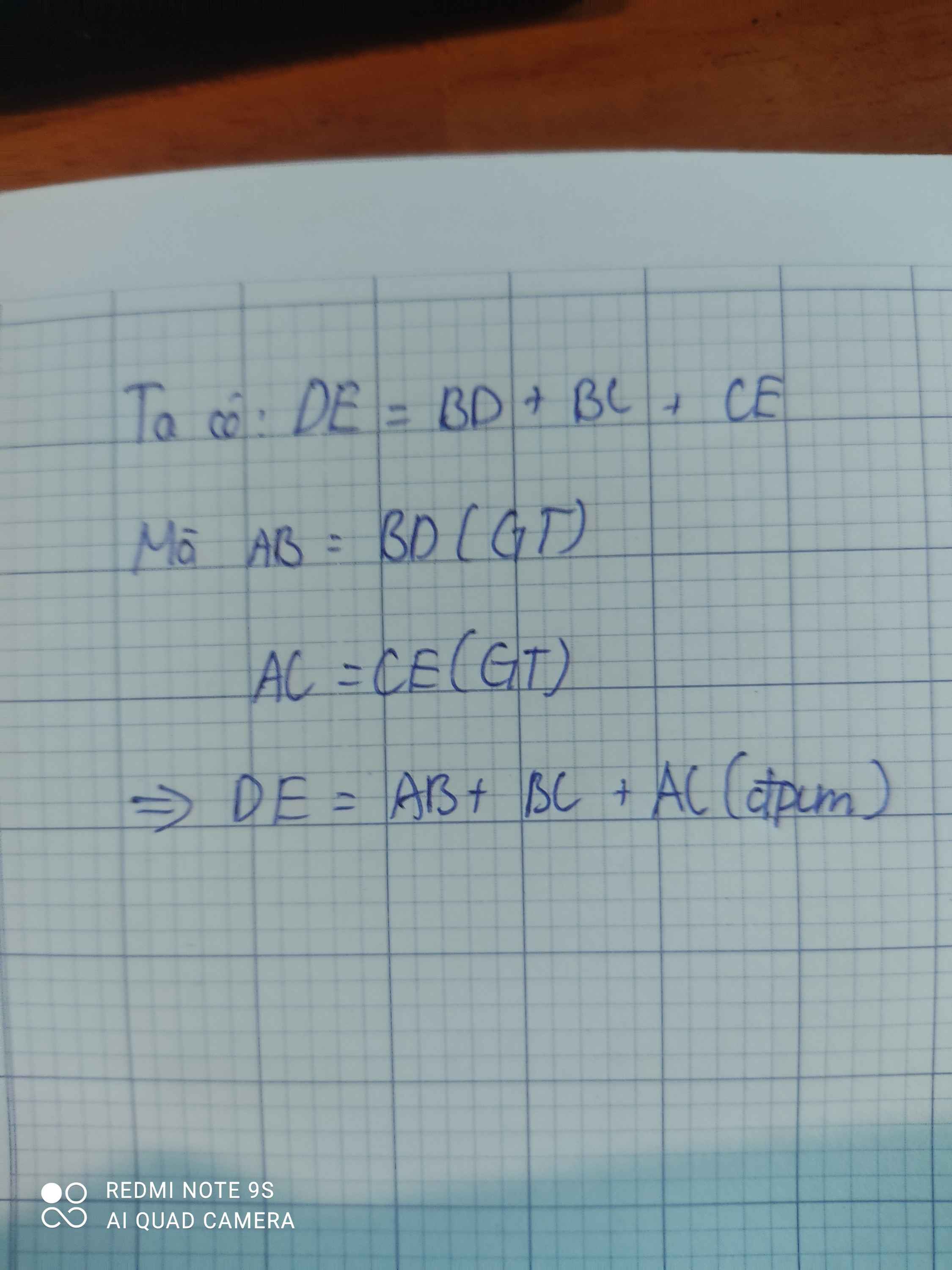

Phần a:
Vì Δ ABC cân ở A
=> ^ABC = ^ACB
và AB = AC mà
^ABD + ^ABC = 180° (kề bù)
và ^ACE + ^ACB =180° (kề bù )
=> ^ABD = ^ACE
Xét ΔABD và ΔACE có:
AB = AC (cmt)
^ABD = ^ACE(cmt)
BD = CE (gt)
=>ΔABD = ΔACE (c.g.c)
=> AD = AE hay ΔADE cân ở A
=> đcpcm
Vì Δ ABC cân ở A
=> ^ABC = ^ACB
và AB = AC mà
^ABD + ^ABC = 180° (kề bù)
và ^ACE + ^ACB =180° (kề bù )
=> ^ABD = ^ACE
Xét ΔABD và ΔACE có:
AB = AC (cmt)
^ABD = ^ACE(cmt)
BD = CE (gt)
=>ΔABD = ΔACE (c.g.c)
=> AD = AE hay ΔADE cân ở A
=>AD=AE (Hai cạnh tương ứng)