Cho tam giác ABC. Các đường trung tuyến BD; CE. Gọi M; N theo thứ tự là trung điểm của BE; CD. Gọi I; K theo thứ tự là giao điểm của MN và BD và CE. Chứng minh MI = IK = KN .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C M D K
từ M vẽ MK// BD ( K thuộc AC )
Tam giác BDC có : M là trung điểm BC; MK//BD
Suy ra : K là trung điểm CD
Do đó: MK là đường trung bình của tam giác BDC.
--> MK = BD/2 = 2AM/2 = AM
---> tam giác AMK cân tại M --> góc MAK = góc MKA
Ta có : góc MAK + góc C = 90 độ
hay góc MKA + góc C = 90 độ
==> góc MKA = 90 độ - góc C (1)
Lại có : góc MKA = góc KMC + góc C = góc DBC + góc C = góc B/2 + góc C = góc C/2 + góc C = 3/2. góc C (2)
Từ (1) (2) ==> 90 độ - góc C = 3/2. góc C
==> 5/2. góc C = 90 độ
==> góc C = 36 độ
==> góc B = 36 độ
==> góc A= 180-36.2=108 độ

G là giao điểm của 2 đường trung tuyến BD và CE
Suy ra : G là trọng tâm tam giác ABC
Suy ra :
GD = 1/3 BD = 1/3 x 24 = 8 ( cm )
GE = 1/3 CE = 1/3 x 45 = 15 ( cm )
Xét tam giác ABC có :
E là trung điểm AB ( trung tuyến CE )
D là trung điểm AC ( trung tuyến BD )
Suy ra : ED là đường trung bình của tam giác ABC
Suy ra ED : = 1/2 x BC = 1/2 x 34 = 17 ( cm )
Vậy GD = 8 cm
GE = 15 cm
ED = 17 cm

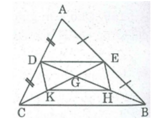
Nếu BD ⊥ CE ⇒ DH ⊥ EK
Hình bình hành DEHK có hai đường chéo vuông góc nên nó là hình thoi.
Con tham khảo tại link dưới đây nhé:
Câu hỏi của Dương Ánh Ngọc - Toán lớp 8 - Học toán với OnlineMath