Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Có S A B C = 1 2 . a . a = a 2 2
Vậy V S . A B C = 1 3 S A . S A B C = a 3 3 6
Đáp án: C
Gọi H là trung điểm BC ⇒ A ' H ⊥ ( A B C )
S ∆ A B C = 1 2 A B . A C = a 2 3 2
Kết luận V = a 3 . a 2 3 2 = 3 a 3 2
1.
\(\overrightarrow{AB}=\left(2;-6\right)\Rightarrow AB=2\sqrt{10}\) \(\Rightarrow BC=AB.cosB=\sqrt{10}\)
Gọi \(C\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(x-1;y-2\right)\\\overrightarrow{BC}=\left(x-3;y+4\right)\end{matrix}\right.\)
Tam giác ABC vuông tại C và có \(BC=\sqrt{10}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AC}.\overrightarrow{BC}=0\\BC^2=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-3\right)+\left(y-2\right)\left(y+4\right)=0\\\left(x-3\right)^2+\left(y+4\right)^2=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2-4x+2y-5=0\\x^2+y^2-6x+8y+15=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3y-10=0\\x^2+y^2-6x+8y+15=0\end{matrix}\right.\)
\(\Rightarrow\left(3y+10\right)^2+y^2-6\left(3y+10\right)+8y+15=0\)
\(\Leftrightarrow2y^2+10y+11=0\)
\(\Leftrightarrow y=...\)
2.
Kẻ \(EF\perp BC\)
\(S_{ABC}=9S_{BDE}\Rightarrow AD.BC=9EF.BD\Rightarrow\dfrac{EF}{AD}=\dfrac{BC}{9BD}\)
Talet: \(\dfrac{EF}{AD}=\dfrac{BF}{BD}=\dfrac{BC}{9BD}\Rightarrow BC=9BF\)
Hệ thức lượng: \(BE^2=BF.BC=9BF^2\Rightarrow BE=3BF\)
\(\Rightarrow cosB=\dfrac{BF}{BE}=\dfrac{1}{3}\)
Gọi R là bán kính đường tròn ngoại tiếp ABC và \(r\) là bán kính đường tròn ngoại tiếp BDE
\(sinB=\sqrt{1-\left(\dfrac{1}{3}\right)^2}=\dfrac{2\sqrt{2}}{3}\)
\(\Rightarrow r=\dfrac{DE}{2sinB}=\dfrac{3}{2}\) (định lý sin tam giác BDE)
Dễ dàng chứng minh 2 tam giác ABC và BDE đồng dạng (chung góc B và \(\widehat{A}=\widehat{BDE}\) vì cùng bù \(\widehat{CDE}\))
Mà \(S_{ABC}=9S_{BDE}\Rightarrow\) 2 tam giác đồng dạng tỉ số \(k=\sqrt{9}=3\)
\(\Rightarrow R=3r=\dfrac{9}{2}\)
a) Xét ΔABC có
BA<BC(gt)
mà góc đối diện với cạnh BA là \(\widehat{ACB}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{BAC}>\widehat{ACB}\)(Quan hệ giữa cạnh và góc đối diện trong tam giác)
b) Xét ΔABH vuông tại H và ΔAMH vuông tại H có
HB=HM(gt)
AH chung
Do đó: ΔABH=ΔAMH(hai cạnh góc vuông)
Suy ra: BA=MA(hai cạnh tương ứng)
Xét ΔBAM có BA=MA(cmt)
nên ΔBAM cân tại A(Định nghĩa tam giác cân)
Xét ΔBAM cân tại A có \(\widehat{B}=60^0\)(gt)
nên ΔBAM đều(Dấu hiệu nhận biết tam giác đều)
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên BA=BE
hay ΔBAE cân tại B
mà \(\widehat{ABE}=60^0\)
nên ΔBAE đều
Trong ΔABC ta có:
∠A + ∠B + ∠C = 180o(tổng ba góc trong tam giác)
⇒∠B = 180o - (∠A +∠C )
⇒x = 180o - (60o + 50o) = 70o
(∠B1) =(∠B2 ) = (1/2 )∠B (vì BD là tia phân giác)
⇒ ∠B1 = ∠B2 = 70o : 2 = 35o
Trong ΔBCD ta có ∠(ADB) là góc ngoài tại đỉnh D
⇒ ∠(ADB) = ∠(B1 ) + ∠C (tính chất góc ngoài tam giác)
Nên ∠(ADB) = 35º + 50º = 85º
+) Do ∠(ADB) + ∠(BDC) = 180o(hai góc kề bù)
⇒∠(BDC) = 180o-∠(ADB) = 180o - 85o = 95o
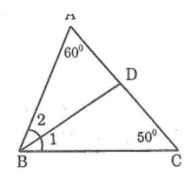
Hình (tự vẽ)
a) ΔACE = ΔAKE
Xét hai tam giác vuông ACE và AKE có:
∠CAE = ∠KAE (AE là phân giác)
AE : cạnh chung
Do đó ΔACE = ΔAKE (cạnh huyền - góc nhọn)
b) EB > AC
Xét tam giác ABC vuông tại C ⇒ ∠A+ ∠B = 90o ⇒ ∠B = 90o - ∠A = 90o - 60o = 30o (1)
Ta có: AE là phân giác của ∠CAK ⇒ ∠CAE = ∠ KAE = ∠CAK : 2 = 60o : 2 = 30o (2)
Từ (1) và (2) suy ra: ΔAEB cân tại E ⇒ EB = EA (hai cạnh đáy) (3)
Mà AE > AC (định lí đường vuông góc là đường ngắn nhất) (4)
Từ (3) và (4) suy ra: EB > AC.
c) AC, DB, KE cùng đi qua một điểm.
Gọi giao của AC và BD là G.
Xét ΔABG có AD, BC là đường cao ⇒ E là trực tâm
⇒ GE ⊥ AB
Mà EK ⊥ AB
Nên G, E, K thẳng hàng
Vậy AC, BD, KE cùng đi qua 1 điểm