Cho tứ giác ABCD trong đó có B ^ = 75 0 ; D ^ = 120 0 . Khi đó A ^ + C ^ = ?
A. 110 0
B. 120 0
C. 220 0
D. 165 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
6 tháng 2 2018
Đúng(0)
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
28 tháng 12 2021
Lời giải:
Ta có: $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0$ (tổng 4 góc trong 1 tứ giác)
$\Rightarrow \widehat{D}=360^0-(\widehat{A}+\widehat{B}+\widehat{C})$
$=360^0-(75^0+115^0+100^0)=70^0$
Đáp án A.
CM
27 tháng 10 2017
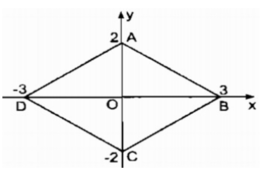
Ta có: A(0;2) và C(0;-2) là hai điểm đối xứng qua O(0;0)
⇒ OA = OC
B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)
⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Lại có: Ox ⊥ Oy hay AC ⊥ BD.
Vậy tứ giác ABCD là hình thoi
Trong ∆ OAB vuông tại O, theo định lý Pi-ta-go ta có:
A B 2 = O A 2 + O B 2
A B 2 = 2 2 + 3 2 = 4 + 9 = 13
AB = 13
Vậy chu vi của hình thoi bằng 4 13
TD
1
LA
1 tháng 4 2018
Bạn kẻ đoạn thẳng AC và BD rồi dùng tổng 3 góc trong tam giác LÀ XONG RỒI
11 tháng 7 2020
a﴿ Kẻ BN vuông AD, BM vuông CD
Xét tam giác vuông BNA và BMD có
: AB = BC ; góc BNA = 180 độ
‐ góc BAD = 70 độ
nên góc BAN = góc BCD = 70 độ
=> tam giác BMD = tam giác BND ﴾cạnh huyền ‐ góc nhọn﴿
=> BN = BM => BD là phân giác góc D
b﴿ Nối B vs D, do AB = AD nên tam giác ABD cân tại A
khi đó góc ADB = ﴾180 ‐110) :2= 35 độ
=> góc ADC = 70 Do góc ADC + góc BAD = 180 => AB // CD
Và góc BCD = góc ADC = 70 độ
=> ABCD là hình thang cân
11 tháng 7 2020
a﴿ Kẻ BN vuông AD, BM vuông CD
Xét tam giác vuông BNA và BMD có
: AB = BC ; góc BNA = 180 độ
‐ góc BAD = 70 độ
nên góc BAN = góc BCD = 70 độ
=> tam giác BMD = tam giác BND ﴾cạnh huyền ‐ góc nhọn﴿
=> BN = BM => BD là phân giác góc D
b﴿ Nối B vs D, do AB = AD nên tam giác ABD cân tại A
khi đó góc ADB = ﴾180 ‐110) :2= 35 độ
=> góc ADC = 70 Do góc ADC + góc BAD = 180 => AB // CD
Và góc BCD = góc ADC = 70 độ
=> ABCD là hình thang cân
5 tháng 8 2023
1: Đặt góc A=a; góc B=b; góc C=c; góc D=d
Theo đề, ta có: a/1=b/2=c/3=d/4 và a+b+c+d=360
Áp dụng tính chất của DTSBN, ta được:
a/1=b/2=c/3=d/4=(a+b+c+d)/(1+2+3+4)=360/10=36
=>a=36; b=72; c=108; d=144
2:
góc C+góc D=360-130-105=230-105=125
góc C-góc D=25 độ
=>góc C=(125+25)/2=75 độ và góc D=75-25=50 độ
3:
góc B=360-57-110-75=118 độ
số đo góc ngoài tại B là:
180-118=62 độ
6 tháng 8 2021
Ta có: A(0;-4) và C(0;4) là hai điểm đối xứng qua O(0;0)
⇒ OA = OC
B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)
⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Lại có: Ox ⊥ Oy hay AC ⊥ BD.
Vậy tứ giác ABCD là hình thoi
Trong Δ∆OAB vuông tại O, theo định lý Pi-ta-go ta có:
AB2=OA2+OB2
AB2=42+32 = 16 + 9 = 25
AB = √25
Vậy chu vi của hình thoi bằng 4√25