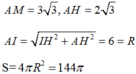Cho hình chóp S.ABC có SA=x; AB=AC=SB=SC=1. Thể tích khối chóp S.ABC lớn nhất khi tổng x+y bằng:
A. 3
B. 2 3
C. 4 3
D. 4 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

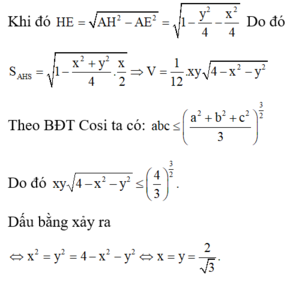

Chọn A.
Do đáy là tam tam giác đều cạnh a nên diện tích đáy là:
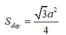
Thể tích khối chóp là:
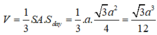

Đáp án là D

• Trong tam giác ABC vuông cân tại B có: A B = B C = A C 2 = a 2
• Đường cao hình chóp: S A = a 3 .Diện tích đáy S ∆ A B C = 1 2 A B . B C = a 2 .
• Thể tích khối chóp: S S . A B C = 1 3 S A S ∆ A B C = a 8 3 3 .

Đáp án B
Gọi H là trung diểm của BC suy ra cos A C B ^ = sin H A B ^ = 1 3 ⇒ cos H A B ^ = 2 2 3
Mà sin B A C ^ = 2 sin H A B ^ . cos H A B ^ = 4 2 9 nên theo định lí Sin, ta có R ∆ A B C = B C 2 s i n B A C ^ = 9 4
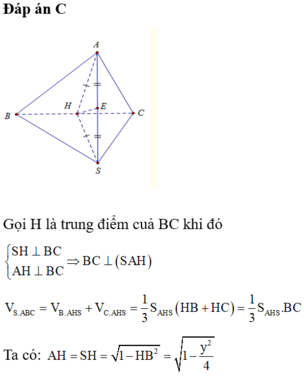
Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là R = R 2 ∆ A B C + S A 2 4 = a 97 4
Vậy diện tích mặt cầu cần tính là S = 4 πR 2 = 4 π a 97 4 2 = 97 πa 2 4

Đáp án C
Thể tích của khối chóp S.ABC có SA, SB, SC đôi một vuông góc nhau là: V = 1 6 S A . S B . S C = a 3 6

Chọn D.
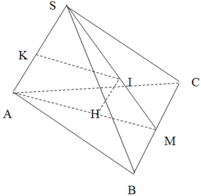
H là tâm của tam giác ABC, M là trung điểm của BC
Trong mp(SAM) dựng đt ss với SA cắt trung trực của SA tại I suy ra I là tâm mặt cầu ngoại tiếp