Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng - 2019 ; 2019 để hàm số y = sin 3 x - 3 cos 2 x + m sin x - 1 đồng biến trên đoạn .
A. 2020.
B. 2019.
C. 2028.
D. 2018.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
TXĐ: D = R
Ta có: y ' = 3 x 2 - 6 x + 3 m
Để hàm số đã cho nghịch biến trên 1 ; 2
thì y ' ≤ 0 , ∀ x ∈ 1 ; 2 và bằng 0 tại hữu hạn điểm
![]()
![]()
![]()
![]()
Hàm số y = x - 1 2 đồng biến trên 1 ; + ∞ nên cũng đồng biến trên 1 ; 2
![]()
![]()
Lại có m ∈ - 10 ; 10 và m ∈ Z nên m ∈ - 10 ; - 9 ; . . ; 0
Vậy có 11 giá trị của m

Chọn B
Phương pháp:
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Ta sử dụng phương trình ![]() có hai nghiệm dương phân biệt
có hai nghiệm dương phân biệt
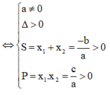
Cách giải:
Ta có ![]()
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Khi đó
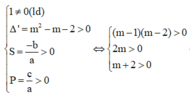
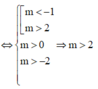
Mà ![]()
![]() nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.
nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.

Ta có:
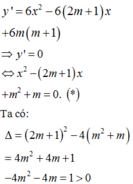
⇒ * luôn có hai nghiệm phân biệt x 1 ; x 2 x 1 < x 2 với mọi m.
Áp dụng hệ thức Vi-ét ta có:
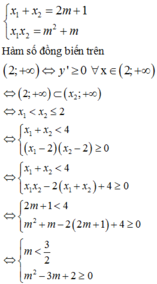
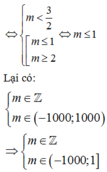
Vậy có tất cả 1001 giá trị m thỏa mãn bài toán.
Chọn B.
Bài toán trở thành tìm m để hàm số y = t 3 + 3 t 2 - m t - 4 đồng biến trên 0 ; 1 .
TXĐ: D = R .
Ta có y ' = 3 t 2 + 6 t - m
Để hàm số đồng biến trên 0 ; 1
ta có TXĐ:
Có 2019 giá trị của m thỏa mãn.
Chọn B.