Hỏi có bao nhiêu giá trị mm nguyên trong nửa khoảng (0; 2017] để phương trình | x 2 − 4|x |−5| − m = 0 có hai nghiệm phân biệt?
A. 2016
B. 2008
C. 2009
D. 2017
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.
mình trình bày hơi dài mong bạn thông cảm 

Chọn B
Phương pháp:
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Ta sử dụng phương trình ![]() có hai nghiệm dương phân biệt
có hai nghiệm dương phân biệt
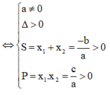
Cách giải:
Ta có ![]()
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Khi đó
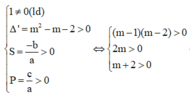
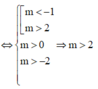
Mà ![]()
![]() nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.
nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.

Ta có: Δ = 4 m − 3 2 − 4.2. 1 − 2 m = 4 m − 1 2
2 x 2 + 2 x 2 − 4 m − 3 x 2 + 2 x + 1 − 2 m = 0 ⇔ x 2 + 2 x = 1 2 ( 1 ) x 2 + 2 x = 2 m − 1 ( 2 )
( 1 ) ⇔ x 2 + 2 x − 1 2 = 0 ⇔ x = − 2 + 6 2 ∉ − 3 ; 0 x = − 2 − 6 2 ∈ − 3 ; 0
2 ⇔ x + 1 2 = 2 m . Phương trình đã cho có đúng 1 nghiệm thuộc đoạn - 3 ; 0 khi và chỉ khi phương trình (2) có nghiệm nhưng không thuộc đoạn - 3 ; 0 hoặc vô nghiệm.
Xét (2), nếu m < 0 thì (2) vô nghiệm (thỏa mãn yêu cầu).
+) Nếu m = 0 thì (2) có nghiệm duy nhất x = - 1 ∈ - 3 ; 0 (không thỏa yêu cầu).
+) Nếu m > 0 thì (2) có hai nghiệm phân biệt x 1 = − 1 − 2 m < − 1 + 2 m = x 2 nên (2) có hai nghiệm không thuộc - 3 ; 0 nếu
− 1 − 2 m < − 3 − 1 + 2 m > 0 ⇔ m > 2 m > 1 2 ⇔ m > 2
Vậy m < 0 m > 2
Mà m ∈ - 2019 ; 2019 và m ∈ Z nên m ∈ - 2018 ; - 2017 ; . . . ; - 1 ; 3 ; 4 ; . . . ; 2018
Số các giá trị của m thỏa mãn bài toán là 2018 + 2016 = 4034.
Đáp án cần chọn là: D

Đáp án A
Để hàm số đồng biến trên khoảng 2 ; + ∞ thì
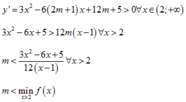
Xét f x = 3 x 2 − 6 x + 5 12 x − 1 có đạo hàm f ' x = 3 x 2 − 6 x + 1 12 x − 1 2 > 0 x > 2
Do đó f(x) đồng biến trên khoảng 2 ; + ∞ hay M i n f x = f 2 = 5 12 ⇒ m < 5 12
Lại có m ∈ − 2017 ; 2017 m ∈ ℤ .
Suy ra có 2018 giá trị của m thỏa mãn

PT: x 2 - 4 x - 5 - m = 0 ⇔ x 2 - 4 x - 5 = m 1
Số nghiệm phương trình (1) bằng số giao điểm của đồ thị hàm số
y = x 2 - 4 x - 5 P và đường thẳng y = m (cùng phương Ox)
Xét hàm số y = x 2 - 4 x - 5 P 1 có đồ thị như hình 1.
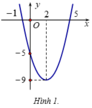
Xét hàm số y = x 2 - 4 x - 5 P 2 là hàm số chẵn nên có đồ thị nhận Oy làm trục đối xứng.
Mà y = x 2 - 4 x - 5 = x 2 - 4 x - 5 nếu x ≥ 0
Suy ra đồ thị hàm số P 2 gồm hai phần:
Phần 1: Giữ nguyên đồ thị hàm số P 1 phần bên phải Oy.
Phần 2: Lấy đối xứng phần 1 qua trục Oy.
Ta được đồ thị P 2 như hình 2.
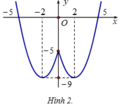
Xét hàm số y = x 2 - 4 x - 5 P , ta có: x 2 − 4 x − 5 ( y ≥ 0 ) − x 2 − 4 x − 5 ( y < 0 )
Suy ra đồ thị hàm số (P) gồm hai phần:
Phần 1: Giữ nguyên đồ thị hàm số P 2 phần trên Ox.
Phần 2: Lấy đối xứng đồ thị hàm số P 2 phần dưới Ox qua trục Ox.
Ta được đồ thị (P) như hình 3.
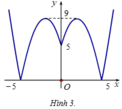
Quan sát đồ thị hàm số (P) ta có:
Phương trình |x2 – 4 |x| − 5| − m = 0 (1) có hai nghiệm phân biệt ⇔ m > 9 m = 0
Mà m ∈ Z m ∈ 0 ; 2017 ⇒ m ∈ 0 ; 10 ; 11 ; 12 ; . . . ; 2017
Vậy có 2009 giá trị nguyên của m thỏa mãn.
Đáp án cần chọn là: C
Đáp án B