Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
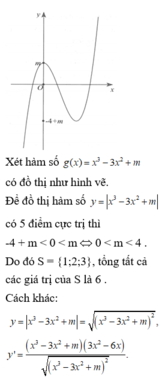
Đồ thị hàm số đã cho có 5 điểm cực trị khi và chỉ khi phương trình y’ = 0 có 5 nghiệm phân biệt và y’ đổi dấu qua 5 nghiệm đó, điều này tương đương với x 3 - 3 x 2 + m có ba nghiệm phân biệt khác 0 và 2
Đáp án B
Xét hàm số f x = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên [0;2] có f ' x = 0 ⇔ x = 2
Tính f 0 = m - 20 ; f 2 = m + 6 → m a x 0 ; 2 y = m a x [ 0 ; 2 ] f x = m - 20 ; m + 6
TH1. Với m a x 0 ; 2 y = m - 20 ⇒ m - 20 ≥ m + 6 m - 20 ≤ 20 ⇔ m ≤ 7 - 20 ≤ m ≤ 20 ⇔ 0 ≤ m ≤ 7
TH2. Với m a x 0 ; 2 y = m + 6 ⇒ m - 20 ≤ m + 6 m + 6 ≤ 20 ⇔ m ≥ 7 - 20 ≤ m + 6 ≤ 20 ⇔ 7 ≤ m ≤ 14
Kết hợp với m ∈ ℤ , ta được m = 0 ; 1 ; 2 ; . . . ; 14 → ∑ m = 105 .
Đáp án C.
Đặt t = sin x , t ∈ − 1 ; 1 . Phương trình đã cho trở thành 2 t + 1 t + 2 = m (*).
Để phương trình đã cho có đúng hai nghiệm thuộc đoạn 0 ; π thì phương trình (*) phải có đúng một nghiệm thuộc nửa khoảng 0 ; 1 .
Xét hàm số f t = 2 t + 1 t + 2 . Ta có f ' t = 3 t + 2 2 .
Bảng biến thiên của :
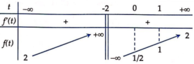
Vậy để phương trình (*) có đúng một nghiệm thuộc nửa khoảng 0 ; 1 thì m ∈ 1 2 ; 1 . Vậy C là đáp án đúng
\(\Leftrightarrow\left(x-y+m\right)^2+y^2+2\left(m+1\right)y-m^2+25\ge0\); \(\forall x;y\)
\(\Leftrightarrow y^2+2\left(m+1\right)y-m^2+25\ge0\) ;\(\forall y\)
\(\Leftrightarrow\Delta'=\left(m+1\right)^2-\left(-m^2+25\right)\le0\)
\(\Leftrightarrow m^2+m-12\le0\Rightarrow-4\le m\le3\)
Phương trình viết lại m + 1 x = 3 m 2 - 1 x = 1 - m
Phương trình đã cho có nghiệm duy nhất khi 3 m 2 - m - 2 ≠ 0 ⇔ m ≠ 1 m ≠ − 2 3
Do m ∈ Z và m ∈ [−5; 10] ⇒ m ∈ {−5; −4; −3; −2; −1; 0; 2; 3; 4; 5; 6; 7; 8; 9; 10}.
Do đó, tổng các phần tử trong S bằng 39.
Đáp án cần chọn là: B