Tính khoảng cách từ điểm M(1; 2; 0) lần lượt đến các mặt phẳng sau: ( γ ): z + 5 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có :
\(V_{M.AB'C}=V_{B'.MAC}=\frac{B'B.S_{ABC}}{3}\)
Mà BB'=A'A=a
\(S_{AMC}=\frac{CD.AM}{2}=\frac{a.2a}{2.3}=\frac{a^2}{3}\)
=> \(V_{M.AB'C}=\frac{a^3}{9}\) (1)
=> dM,(AB'C)=\(\frac{3.V_{M.AB'C}}{S_{AB'C}}\) (2)
tam giác AB'C cps \(AB=B'C=2\sqrt{3}\)
và \(AB=a\sqrt{2}\)
=>\(S_{AB'C}=\frac{a^2\sqrt{5}}{2}\) (3)
Từ (1), (2)&(3)
=> dM;(AB'C)=\(\frac{2a}{3\sqrt{a}}\)
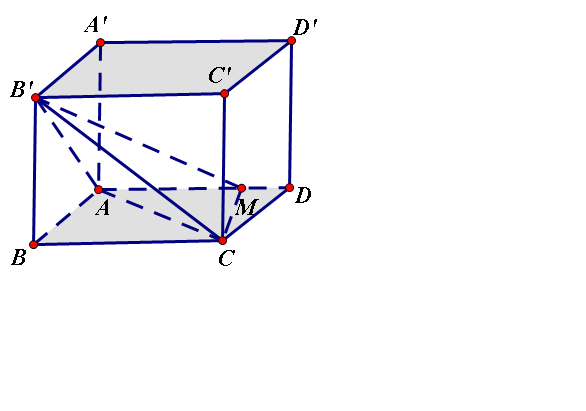
Pytago tính đuợc 3 cạnh ΔAMC
\(AC=a\sqrt{5}\); \(AM=\frac{3a}{2}\), \(MC=\frac{a\sqrt{5}}{2}\)
Dùng công thức HeronHeron =>\(S_{AMC}=\frac{3a^2}{4}\)
\(V_{M.AB'C}=V_{B.AB'C}=\frac{a^3}{4}\)
Mặt khác dùng công thức HeronHeron cũng tính được \(S_{AB'C}=\frac{3a^2}{2}\)
=> \(d_{\left(M;\left(AB'C\right)\right)}=\frac{3V_{M.AB'C}}{S_{AB'C}}=\frac{a}{2}\)

Lời giải:
$x=-2+t; y=1+2t$
$\Rightarrow 2x-y=2(-2+t)-(1+2t)=-5$
$\Leftrightarrow 2x-y+5=0$
Khoảng cách từ điểm $M$ đến $(\Delta)$ là:
\(\frac{|2.3-(-1)+5|}{\sqrt{2^2+(-1)^2}}=\frac{12\sqrt{5}}{5}\)

Ta có: \(B_M=2.10^{-7}.\dfrac{I_M}{r_M}=2.10^{-7}.\dfrac{I}{2r_N}\) (1)
\(B_N=2.10^{-7}.\dfrac{I_N}{r_N}=2.10^{-7}.\dfrac{I}{r_N}\) (2)
Từ (1) , (2) => \(\dfrac{B_M}{B_N}=\dfrac{1}{2}\Rightarrow B_N=2B_M=4.10^{-5}\left(T\right)\)

Đáp án D
Khi dịch chuyển nguồn theo phương song song với hai khe thì hệ vân (vân trung tâm ) dịch chuyển theo chiều ngược lại một đoạn :
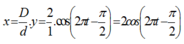
Chu kì dao động là : T = 1s.
Khoảng vân : 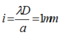
Điểm M cách vị trí trung tâm 1mm, vậy ban đầu khi t = 0 thì M là vân sáng.
Điểm M là vân sáng thì thỏa mãn : xM = ki
Ta thấy vân trung tâm sẽ dao động với biên độ 2 cm (từ phương trình), vậy điểm M sẽ là vân sáng khi vân trung tâm ở các vị trí có tọa độ x = 0, 1, 2, – 1, –2 cm
Vẽ đường tròn ta được:
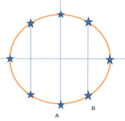
Các vị trí đánh dấu sao là các vị trí trong một chu kì chuyển động M là vân sáng. Ban đầu M nằm ở vị trí A. mỗi chu kì có 8 lần M là vân sáng
Vậy khi M à vân sáng lần thứ 2018 = 8.252 + 2 lần thì nó đã đi trong thời gian là : t = 252T + ∆t
Dễ thấy khi đi được 252 chu kì thì M đã quay lại A, vậy chỉ cần đi đến B là đã được thêm 2 lần nữa ( vì ban đầu khi t = 0 thì M ở A, nên nó là 1 vân sáng, đến lúc nó đến B được tính là lần nữa).
Thời gian đi hết cung AB là :
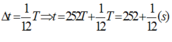


d(M,( γ )) = 5