1) Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = f(x) = \(\frac{mx^3}{3}+7mx^2+14x-m+2\) giảm trên nửa khoảng [1; +∞)
2) Tìm tất cả các giá trị thực của tham số m sao cho hàm số y=f(x) = x + mcosx luôn đồng biến trên R?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Tập xác định D = R, yêu cầu của bài toán đưa đến giải bất phương trình
![]()
Tương đương với
![]()
Dễ dàng có được g(x) là hàm tăng ![]()
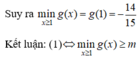
![]()

Chọn đáp án D
![]() .
.
Ta có y ' = m 2 - 4 x + m 2 .
Hàm số luôn đơn điệu trên từng khoảng - ∞ ; - m và - m ; + ∞ .
Hàm số giảm trên khoảng - ∞ ; 1 tức là hàm số nghịch biến trên khoảng - ∞ ; 1 .
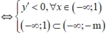
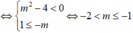

1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)

Đáp án D
Điều kiện: x ≠ m .
Đạo hàm y ' = − m 2 + 4 x − m 2 ;
Hàm số đồng biến trên khoảng 1 ; + ∞ ⇔ y ' > 0, ∀ x ∈ 1 ; + ∞ x ≠ m
⇔ − m 2 + 4 > 0, ∀ x ∈ 1 ; + ∞ x ≠ m ⇔ − 2 < m < 2 m ∉ 1 ; + ∞ ⇔ m ∈ − 2 ; 1
Câu 1:
\(y'=f\left(x\right)=mx^2+14mx+14\)
- Với \(m=0\Rightarrow y'=14>0\Rightarrow y\) đồng biến trên R (ko thỏa mãn)
- Với \(m\ne0\) để hàm số nghịch biến trên \(\left[1;+\infty\right]\) ta có các trường hợp sau:
TH1: \(\left\{{}\begin{matrix}m< 0\\\Delta'=49m^2-14m\le0\end{matrix}\right.\) \(\Rightarrow\) ko tồn tại m thỏa mãn
TH2: \(\left\{{}\begin{matrix}m< 0\\\Delta'>0\\x_1< x_2\le1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\m.f\left(1\right)\ge0\\\frac{x_1+x_2}{2}< 1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\m\left(15m+14\right)\ge0\\-7< 1\end{matrix}\right.\) \(\Rightarrow m\le-\frac{14}{15}\)
Câu 2:
\(y'=1-msinx\)
Để hàm số đồng biến trên R \(\Leftrightarrow1-m.sinx\ge0\) \(\forall x\)
\(\Leftrightarrow msinx\le1\)
- Với \(m=0\Rightarrow0< 1\) (đúng)
- Với \(m< 0\Rightarrow sinx\ge\frac{1}{m}\Rightarrow\frac{1}{m}\le\min\limits_{x\in R}\left(sinx\right)=-1\)
\(\Rightarrow\frac{m+1}{m}\le0\Rightarrow-1\le m< 0\)
- Với \(m>0\Rightarrow sinx\le\frac{1}{m}\Rightarrow\frac{1}{m}\ge\max\limits_{x\in R}\left(sinx\right)=1\)
\(\Rightarrow\frac{1-m}{m}\ge0\Rightarrow0< m\le1\)
Kết hợp lại ta được \(-1\le m\le1\)