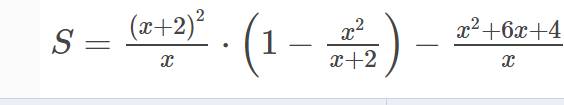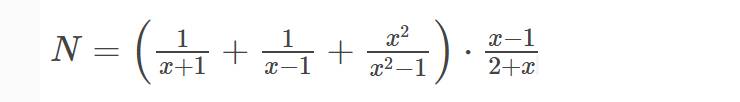bài 2 : Tính giá trị biểu thức
A; ( 7/8 - 3/4 ) . 1 1/3 - 2/7 . ( 3.5 ) ^2 = ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
0
Những câu hỏi liên quan
10 tháng 3 2021
Bài 1 :
\(N=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
Ta có : \(x+y+z=0\Rightarrow x+y=-z;y+z=-x;x+z=-y\)
hay \(-z.\left(-x\right)\left(-y\right)=-zxy\)
mà \(xyz=2\Rightarrow-xyz=-2\)
hay N nhận giá trị -2
Bài 2 :
\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)Đặt \(a=10k;b=3k\)
hay \(\frac{30k-6k}{10k-9k}=\frac{24k}{k}=24\)
hay biểu thức trên nhận giá trị là 24
c, Ta có : \(a-b=3\Rightarrow a=3+b\)
hay \(\frac{3+b-8}{b-5}-\frac{4\left(3+b\right)-b}{3\left(3+b\right)+3}=\frac{-5+b}{b-5}-\frac{12+4b-b}{9+3b+3}\)
\(=\frac{-5+b}{b-5}-\frac{12+3b}{6+3b}\)quy đồng lên rút gọn, đơn giản rồi
NC
10 tháng 3 2021
1.Ta có:\(x+y+z=0\)
\(\Rightarrow\hept{\begin{cases}x+y=-z\\y+z=-x\\x+z=-y\end{cases}}\)
\(\Rightarrow N=\left(x+y\right)\left(y+z\right)\left(x+z\right)=\left(-z\right)\left(-x\right)\left(-y\right)=-2\)
2.Ta có:\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)
Đặt \(\frac{a}{10}=\frac{b}{3}=k\Rightarrow a=10k;b=3k\)
Ta có:\(A=\frac{3a-2b}{a-3b}=\frac{3.10k-2.3k}{10k-3.3k}=\frac{30k-6k}{10k-9k}=\frac{k\left(30-6\right)}{k\left(10-9\right)}=24\)
Vậy....
14 tháng 3 2022
a: \(A=0x^2y^4z+\dfrac{7}{2}x^2y^4z-\dfrac{2}{5}x^2y^4z=\dfrac{31}{10}x^2y^4z=\dfrac{31}{10}\cdot2^2\cdot\dfrac{1}{16}\cdot\left(-1\right)=-\dfrac{31}{40}\)
a: \(=\dfrac{7}{5}x^4z^3y=\dfrac{7}{5}\cdot2^4\cdot\left(-1\right)^3\cdot\dfrac{1}{2}=-\dfrac{56}{5}\)
b: \(=-xy^3\)
7 tháng 3 2022
Bài 4:
b: \(=x^2z\left(-1+3-7\right)=-5x^2z=-5\cdot\left(-1\right)^2\cdot\left(-2\right)=10\)
c: \(=xy^2\left(5+0.5-3\right)=2.5xy^2=2.5\cdot2\cdot1^2=5\)
30 tháng 3 2022
a: \(A=5\cdot2\cdot\left(-3\right)-10+3\cdot\left(-3\right)=-30-10-9=-49\)
b: \(B=8\cdot1\cdot\left(-1\right)^2-1\cdot\left(-1\right)-2\cdot1-10\)
=8+1-2-10
=-3
T
22 tháng 12 2023
a) ĐKXĐ: \(x\ne0;x\ne-2\)
b) \(S=\dfrac{\left(x+2\right)^2}{x}\cdot\left(1-\dfrac{x^2}{x+2}\right)-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{\left(x+2\right)^2}{x}\cdot\dfrac{x+2-x^2}{x+2}-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{\left(x+2\right)\left(x+2-x^2\right)}{x}-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{x^2+2x-x^3+2x+4-2x^2-x^2-6x-4}{x}\)
\(=\dfrac{-x^3-2x^2-2x}{x}\)
\(=\dfrac{x\left(-x^2-2x-2\right)}{x}\)
\(=-x^2-2x-2\)
Với \(x=0\Rightarrow\) loại
Với \(x=1\), thay vào \(S\) ta được
\(S=-1^2-2\cdot1-2=-5\)
c) Có: \(S=-x^2-2x-2\)
\(=-\left(x^2+2x+2\right)\)
\(=-\left(x^2+2x+1\right)-1\)
\(=-\left(x+1\right)^2-1\)
Ta thấy: \(\left(x+1\right)^2\ge0\forall x\ne0;x\ne-2\)
\(\Rightarrow-\left(x+1\right)^2\le0\forall x\ne0;x\ne-2\)
\(\Rightarrow S=-\left(x+1\right)^2-1\le-1\forall x\ne0;x\ne-2\)
Dấu \("="\) xảy ra khi: \(x+1=0\Leftrightarrow x=-1\left(tmdk\right)\)
\(\text{#}\mathit{Toru}\)
LT
1
23 tháng 12 2023
a: ĐKXĐ: \(x\notin\left\{1;-1;-2\right\}\)
b: \(N=\left(\dfrac{1}{x+1}+\dfrac{1}{x-1}+\dfrac{x^2}{x^2-1}\right)\cdot\dfrac{x-1}{x+2}\)
\(=\left(\dfrac{1}{x+1}+\dfrac{1}{x-1}+\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{x-1}{x+2}\)
\(=\dfrac{x-1+x+1+x^2}{\left(x+1\right)\left(x-1\right)}\cdot\dfrac{x-1}{x+2}\)
\(=\dfrac{x^2+2x}{\left(x+2\right)\left(x+1\right)}=\dfrac{x}{x+2}\)
c: |x|=2
=>x=2(nhận) hoặc x=-2(loại)
Thay x=2 vào N, ta được:
\(N=\dfrac{2}{2+2}=\dfrac{2}{4}=\dfrac{1}{2}\)
KV
5 tháng 10 2023
Bài 5
a) A = -x³ + 6x² - 12x + 8
= -x³ + 3.(-x)².2 - 3.x.2² + 2³
= (-x + 2)³
= (2 - x)³
Thay x = -28 vào A ta được:
A = [2 - (-28)]³
= 30³
= 27000
b) B = 8x³ + 12x² + 6x + 1
= (2x)³ + 3.(2x)².1 + 3.2x.1² + 1³
= (2x + 1)³
Thay x = 1/2 vào B ta được:
B = (2.1/2 + 1)³
= 2³
= 8
KV
5 tháng 10 2023
Bài 6
a) 11³ - 1 = 11³ - 1³
= (11 - 1)(11² + 11.1 + 1²)
= 10.(121 + 11 + 1)
= 10.133
= 1330
b) Đặt B = x³ - y³ = (x - y)(x² + xy + y²)
= (x - y)(x² - 2xy + y² + 3xy)
= (x - y)[(x - y)² + 3xy]
Thay x - y = 6 và xy = 9 vào B ta được:
B = 6.(6² + 3.9)
= 6.(36 + 27)
= 6.63
= 378