\(F\left(x\right)=x^3+x^2+a\) ; \(G\left(x\right)=x+2\)
Tìm a để F(x) chia hết cho G(x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 11 2023
a: \(\lim\limits_{x\rightarrow3^+}f\left(x\right)=\lim\limits_{x\rightarrow3^+}x^2-3=3^2-3=6\)
\(\lim\limits_{x\rightarrow3^-}f\left(x\right)=\lim\limits_{x\rightarrow3^-}x+3=3+3=6\)
b: Vì \(\lim\limits_{x\rightarrow3^+}f\left(x\right)=\lim\limits_{x\rightarrow3^-}f\left(x\right)=6\)
nên hàm số tồn tại lim khi x=3
=>\(\lim\limits_{x\rightarrow3}f\left(x\right)=6\)
11 tháng 9 2021
\(a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2\)
AH
Akai Haruma
Giáo viên
11 tháng 9 2021
Lời giải:
a. $f'(x)\leq 0$
$\Leftrightarrow 3x^2-6x\leq 0$
$\Leftrightarrow x(x-2)\leq 0$
$\Leftrightarrow 0\leq x\leq 2$
b.
$f'(x)=x^2-3x+2=0$
$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$
$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
c.
$g(x)=f(1-2x)+x^2-x+2022$
$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$
$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$
$g'(x)\geq 0$
$\Leftrightarrow -24x^2+2x+5\geq 0$
$\Leftrightarrow (5-12x)(2x-1)\geq 0$
$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$
4 tháng 4 2017
Lời giải:
a) Ta có f'(x) = 3x2 + 1, g(x) = 6x + 1. Do đó
f'(x) > g'(x) <=> 3x2 + 1 > 6x + 1 <=> 3x2 - 6x >0
<=> 3x(x - 2) > 0 <=> x > 2 hoặc x > 0 <=> x ∈ (-∞;0) ∪ (2;+∞).
b) Ta có f'(x) = 6x2 - 2x, g'(x) = 3x2 + x. Do đó
f'(x) > g'(x) <=> 6x2 - 2x > 3x2 + x <=> 3x2 - 3x > 0
<=> 3x(x - 1) > 0 <=> x > 1 hoặc x < 0 <=> x ∈ (-∞;0) ∪ (1;+∞).
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2022
\(f^3\left(2-x\right)-2f^2\left(2+3x\right)+x^2g\left(x\right)+36x=0\) (1)
Thay \(x=0\Rightarrow f^3\left(2\right)-2f^2\left(2\right)=0\Rightarrow\left[{}\begin{matrix}f\left(2\right)=0\\f\left(2\right)=2\end{matrix}\right.\)
Đạo hàm 2 vế của (1):
\(\Rightarrow-3f^2\left(2-x\right).f'\left(2-x\right)-12f\left(2+3x\right).f'\left(2+3x\right)+2x.g\left(x\right)+x^2.g'\left(x\right)+36=0\)
Thay \(x=0\)
\(\Rightarrow-3f^2\left(2\right).f'\left(2\right)-12f\left(2\right).f'\left(2\right)+36=0\)
TH1: \(f\left(2\right)=0\Rightarrow36=0\) (ktm)
TH2: \(f\left(2\right)=2\)
\(\Rightarrow-3.2^2.f'\left(2\right)-12.2.f'\left(2\right)+36=0\Rightarrow f'\left(2\right)=1\)
\(\Rightarrow A=3.2+4.1=10\)
15 tháng 4 2017
a) Ta lập bảng xét dấu
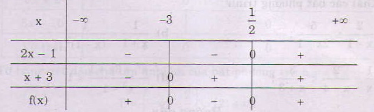
Kết luận: f(x) < 0 nếu - 3 < x <
f(x) = 0 nếu x = - 3 hoặc x =
f(x) > 0 nếu x < - 3 hoặc x > .
b) Làm tương tự câu a).
f(x) < 0 nếu x ∈ (- 3; - 2) ∪ (- 1; +∞)
f(x) = 0 với x = - 3, - 2, - 1
f(x) > 0 với x ∈ (-∞; - 3) ∪ (- 2; - 1).
c) Ta có: f(x) =
Làm tương tự câu b).
f(x) không xác định nếu x = hoặc x = 2
f(x) < 0 với x ∈ ∪
f(x) > 0 với x ∈ ∪ (2; +∞).
d) f(x) = 4x2 – 1 = (2x - 1)(2x + 1).
f(x) = 0 với x =
f(x) < 0 với x ∈
f(x) > 0 với x ∈ ∪
7 tháng 4 2017
a) 3x^3 -10x+3 =(3x-1)(x-3)
| x | -vc | 1/3 | 5/4 | 3 | +vc | |||||||||
| 3x-1 | - | 0 | + | + | + | + | + | |||||||
| x-3 | - | - | - | - | - | 0 | + | |||||||
| 4x-5 | - | - | - | 0 | + | + | + | |||||||
| VT | - | 0 | + | 0 | - | 0 | + |
Kết luận
VT< 0 {dấu "-"} khi x <1/3 hoắc 5/4<x<3
VT>0 {dấu "+"} khi x 1/3<5/4 hoặc x> 3
VT=0 {không có dấu} khi x={1/3;5/4;3}
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) \(f\left( x \right) = 2{x^2} + 4x + 2\) có \(\Delta = 0\), có nghiệm kép là \({x_1} = {x_2} = - 1\)
và \(a = 2 > 0\)
Ta có bảng xét dấu như sau:
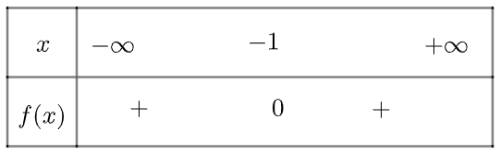
Vậy \(f\left( x \right)\) dương với mọi \(x \ne - 1\)
b) \(f\left( x \right) = - 3{x^2} + 2x + 21\) có \(\Delta = 256 > 0\), hai nghiệm phân biệt là \({x_1} = - \frac{7}{3};{x_2} = 3\)
và \(a = - 3 < 0\)
Ta có bảng xét dấu như sau:
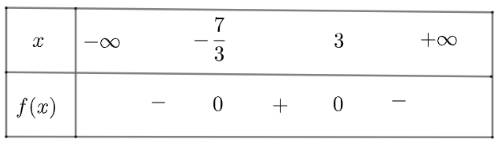
Vậy \(f\left( x \right)\) dương với \(x \in \left( { - \frac{7}{3};3} \right)\) và âm khi \(x \in \left( { - \infty ; - \frac{7}{3}} \right) \cup \left( {3; + \infty } \right)\)
c) \(f\left( x \right) = - 2{x^2} + x - 2\) có \(\Delta = - 15 < 0\), tam thức vô nghiệm
và \(a = - 2 < 0\)
Ta có bảng xét dấu như sau:
Vậy \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\)
d) \(f\left( x \right) = - 4x\left( {x + 3} \right) - 9 = - 4{x^2} - 12x - 9\) có \(\Delta = 0\), tam thức có nghiệm kép \({x_1} = {x_2} = - \frac{3}{2}\) và \(a = - 4 < 0\)
Ta có bảng xét dấu như sau
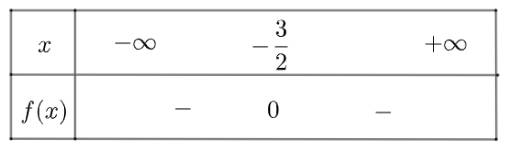
Vậy \(f\left( x \right)\) âm với mọi \(x \ne - \frac{3}{2}\)
e) \(f\left( x \right) = \left( {2x + 5} \right)\left( {x - 3} \right) = 2{x^2} - x - 15\) có \(\Delta = 121 > 0\), có hai nghiệm phân biệt \({x_1} = - \frac{5}{2};{x_2} = 3\) và có \(a = 2 > 0\)
Ta có bảng xét dấu như sau
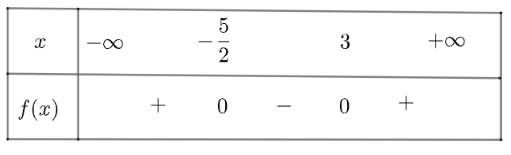
Vậy \(f\left( x \right)\) âm với \(x \in \left( { - \frac{5}{2};3} \right)\) và dương khi \(x \in \left( { - \infty ; - \frac{5}{2}} \right) \cup \left( {3; + \infty } \right)\)
x^3 + x^2 + a x + 2 x^2 - x + 2 x^3 + 2x^2 - x^2 + a -x^2 - 2x 2x + a 2x + 4 a - 4 -
Để \(f\left(x\right)⋮g\left(x\right)\Leftrightarrow a-4=0\Leftrightarrow a=4\)
Vậy a= 4 thì f(x) chia hết cho g(x)
mk có thể tự chia ko ,mk chia r mà nó lại bị lỗi .